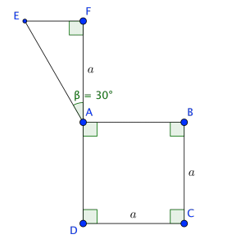
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục (DF )
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(EF = AF.\tan \beta = a.\tan {30^ \circ } = \frac{{a\sqrt 3 }}{3}\)
Khi quay quanh trục DF, tam giác AEF tạo ra một hình nón có thể tích
\( {V_1} = \frac{1}{3}\pi .E{F^2}.AF = \frac{1}{3}\pi .{\left( {\frac{{a\sqrt 3 }}{3}} \right)^2}.a = \frac{{\pi {a^3}}}{9}\)
Khi quay quanh trục DF, hình vuông ABCD tạo ra một hình trụ có thể tích
\( {V_2} = \pi .D{C^2}.BC = \pi .{a^2}.a = \pi {a^3}\)
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF là
\( V = {V_1} + {V_2} = \frac{{\pi {a^3}}}{9} + \pi {a^3} = \frac{{10}}{9}\pi {a^3}\)
Câu hỏi liên quan
-
Cho hai hình vuông cùng có cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ bên). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
-
Một hình trụ có bán kính đáy \(r = 5{\rm{cm}}\), chiều cao \(h = 7{\rm{cm}}\). Tính diện tích xung quang của hình trụ.
-
Cho hình chữ nhật ABCD có AB = 3,BC = 4. Gọi V1,V2 lần lượt là thể tích của các khối trụ sinh ra khi quay hình chữ nhật quanh trục AB và BC. Khi đó tỉ số \( \frac{{{V_1}}}{{{V_2}}} \)
-
Khối trụ tròn xoay có thể tích bằng \(144\pi \) và có bán kính đáy bằng 6. Đường sinh của khối trụ bằng
-
Tính theo $a$ thể tích của một khối trụ có bán kính là a và chiều cao là 2a.
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB =3, AD = 4 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC và mặt phẳng đáy là \(45^0\). Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
-
Cho tam giác ABC vuông tại A, AH là đường cao. Khi quay các cạnh của tam giác ABC quanh cạnh BC thì số hình nón được tạo thành là mấy hình?
-
Cho tam giác đều ABC cạnh a quay quanh đường cao AH tạo nên một hình nón Diện tích xung quanh S của hình nón đó là:
-
Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:
-
Thể tích V của khối trụ có chiều cao bằng a và đường kính đáy bằng \(a\sqrt2\) là?
-
Một hình trụ tròn xoay, bán kính đáy bằng R, trục \(OO'={R\sqrt6\over2}\) . Một đoạn thẳng \(AB = R\sqrt2 \)với \(A\in(O),B\in(O')\). Góc giữa AB và trục hình trụ là
-
Một hình trụ có bán kính đáy R và có thiết diện qua trục là một hình vuông. Tính thể tích của khối lăng trụ tứ giác đều nội tiếp trong khối trụ đã cho.
-
Tính diện tích toàn phần Stp của hình trụ tạo thành khi quay hình chữ nhật (ABCD ) quanh cạnh (AB ), biết (AB = 5 ), (BC = 2 ).
-
Cho hình trụ có diện tích xung quanh bằng \(2{\rm{\pi }}{a^2}\) và bán kính đáy bằng a. Độ dài đường sinh của hình trụ đã cho bằng
-
Mệnh đề nào sau đây là sai?
-
Cho khối nón có chu vi đường tròn đáy là khối nón là \(6\pi\) , chiều cao bằng \(\sqrt7\). Thể tích của
-
Cắt một khối trụ bởi một mặt phẳng ta được một khối \(\left( H \right)\) như hình vẽ. biết rằng thiết diện là một elip có độ dài trục lớn là \(10\), khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất tới mặt đáy lần lượt là 8 và \(14\). Tính thể tích của \(\left( H \right)\)
.PNG)
-
Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2m,3m,2m lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo nước hình trụ có chiều cao là 5cm và bán kính đường tròn đáy là 4cm. Trung bình một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau bao nhiêu ngày thì bể hết nước biết rằng ban đầu bể đầy nước?
-
Một hình trụ có bán kính đáy r =5 cm, chiều cao h=7cm . Diện tích xung quanh của hình trụ này là
-
Cho hai điểm M,N cố định và đường thẳng (\(\Delta\) ) cố định thỏa mãn MN vuông góc \(\Delta\) ,\(d(M,\Delta ) = d( N,\Delta )\). Có bao nhiêu đường tròn đi qua M,N và nhận (\(\Delta \)) làm trục?
