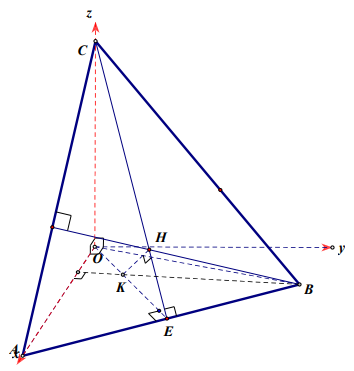
Trong không gian, cho tam giác OAB cân ở O có \(O A=O B=5 ; \tan \widehat{A O B}=\frac{4}{3}\) . Điểm C di động trên tia Oz vuông góc (OAB) , gọi H là trực tâm của tam giác ABC . Khi C di động trên tia Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng: 

Trong không gian với hệ tọa độ Oxyz, cho điểm \(A\left( {1;0;2} \right)\) và đường thẳng \(d:\frac{{x – 1}}{1} = \frac{y}{1} = \frac{{z + 1}}{2}\). Đường thẳng \(\Delta \) đi qua A, vuông góc và cắt d có phương trình là

Cho đường thẳng d đi qua điểm A(1;4;-7) và vuông góc với mặt phẳng \((\alpha): x+2 y-2 z-3=0\) . Phương trình chính tắc của đường thẳng d là
 

Trong không gian Oxyz, lập phương trình tham số của đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau: (P): x + y + z - 1 = 0, (Q): 3x + 2y + z + 1 = 0

Trong không gian với hệ tọa độ Oxyz , cho điểm M (2;-1;3) và mặt phẳng (P): x+3y-z+2=0 Đường thẳng d qua điểm M và vuông góc với mặt phẳng (P) có phương trình là
 

Cho đường thẳng  \(\left( d \right):\frac{{x - 2}}{2} = \frac{{y - 2}}{1} = \frac{z}{2}\) và điểm A(2;3;1). Phương trình mặt phẳng (P) chứa A và (d) là

Trong không gian tọa độ Oxyz cho 4 điểm \(A\,(m-1;m;2m-1);\,\,B\,(-1;0;2);\,\,C\,(-1;1;0);\,\,D\,(2;1;-2).\) Biết thể tích của tứ diện ABCD bằng \(\frac{5}{6}\). Tổng tất cả các giá trị của tham số m thỏa mãn yêu cầu bài toán là:

Trong không gian Oxyz, cho điểm \(A\left( {1;2; – 1} \right)\) và mặt phẳng \(\left( P \right):x–y + 2z–3 = 0\). Đường thẳng d đi qua A và vuông góc với mặt phẳng \(\left( P \right)\) có phương trình là

Trong  không  gian  với  hệ  tọa  độ   Oxyz ,  tìm  tọa  độ  tâm I và  bán  kính R của  
mặt  cầu \(( S ) : ( x -1)^2 + y^2 + ( z +1)^2 = 4 .\)

Cho mặt phẳng \((P): x-2 y+z-3=0 \text { và điểm } A(1 2 ; 0)\), phương trình đường thẳng qua A và vuông góc với (P) là
 

Trong không gian Oxyz, cho ba điểm \(A\left( { – 3\,;2\,  ;2} \right),B\left( {0\,; – 1\,;2} \right),C\left( {1\,;1\,;3} \right)\), một vectơ chỉ phương của đường thẳng \(\Delta \) đi qua C và song song với AB có tọa độ là

Trong không gian với hệ tọa độ Oxyz , tính bán kính  R  của mặt cầu \((S ) :x^2 + y^2 + z^2 - 2x - 4y = 0\)

Trong không gian Oxyz, cho hình nón đỉnh \(S\left( {\frac{{17}}{{18}}; – \frac{{11}}{9};\frac{{17}}{{18}}} \right)\) có đường tròn đáy đi qua ba điểm \(A\left( {1;0;0} \right),B\left( {0; – 2;0} \right),C\left( {0;0;1} \right)\). Tính độ dài đường sinh l của hình nón đã cho.

Trong không gian Oxyz, cho điểm \(A\left( {0;1; – 2} \right)\), mặt phẳng \(\left( P \right):x + y + z + 1 = 0\) và mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x – 4y – 7 = 0\). Gọi \(\Delta \) là đường thẳng đi qua A và \(\Delta \) nằm trong mặt phẳng \(\left( P \right)\) và cắt mặt cầu \(\left( S \right)\) tại hai điểm B, C sao cho tam giác IBC có diện tích lớn nhất, với I là tâm của mặt cầu \(\left( S \right)\). Phương trình của đường thẳng \(\Delta \) là

Trong không gian Oxyz , mặt câu tâm I(1 ; 2 ; 3) và đi qua điểm A(1 ; 1 ; 2) có phương trình là

Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD có tọa độ đỉnh \(A(2 ; 0 ; 0), B(0 ; 4 ; 0),C(0 ; 0 ; 6), D(2 ; 4 ; 6)\) .Gọi (S) là mặt cầu ngoại tiếp tứ diện ABCD . Viết phương trình mặt cầu (S') có tâm trùng với tâm của mặt cầu (S) và có bán kính gấp 2 lần bán kính của mặt cầu (S)

Trong không gian Oxyz, cho đường thẳng d: \(\left\{ \begin{array}{l}
x = t\\
y = 1 - t\\
z = 2 + t
\end{array} \right.\). Đường thẳng d đi qua điểm nào sau đây:

Trong không gian Oxyz, một vectơ chỉ phương của đường thẳng chứa trục Oy có tọa độ là

Trong không gian Oxyz , cho đường thẳng \(d:\left\{ \begin{array}{l} x = 1 \\ y = 2 + 3t\\ z = 5-t \end{array} \right.\) Tọa độ một vectơ chỉ phương của d là?

Trong không gian Oxyz cho đường thẳng : \(d: \frac{x-1}{2}=\frac{y+2}{-1}=\frac{z+1}{1}\). Trong các mặt phẳng dưới đây, tìm một mặt phẳng vuông góc với đường thẳng d

Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;1 ;-3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz.