Xét các số phức z thỏa mãn \(|z|=2\). Số phức \(\mathrm{w}=z+3 i\) có mô-đun nhỏ nhất và lớn nhất lần lượt
là m và M . Tổng M+m bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(z=x+y i \text { với } x, y \in \mathbb{R}\) .
Khi đó \(|z|=2 \Leftrightarrow x^{2}+y^{2}=4\) .
Gọi M là điểm biểu diễn hình học của số phức z ta có \(M \in(O ; 2)\)
\(\begin{aligned} &\text { Xét }|\mathrm{w}|=|z+3 i|=\sqrt{x^{2}+(y+3)^{2}}\\ &\text { Goi } A(0 ;-3) \text { suy ra }|\mathrm{w}|=|z+3 i|=\sqrt{x^{2}+(y+3)^{2}}=A M \end{aligned}\).
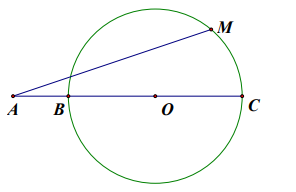
Dễ thấy \(A O=3>2\) nên A nằm ngoài (O;2)
Kẻ đường thẳng AO cắt đường tròn (O;2) tại BC, như hình vẽ.
\(\text { Có } A B \leq A M \leq A C \text { nên }\left\{\begin{array}{l} A M_{\max }=A C=A O+O C=3+2=5 \\ A M_{\min }=A B=A O-O B=3-2=1 \end{array} \Rightarrow\left\{\begin{array}{l} M=5 \\ m=1 \end{array} \Rightarrow M+m=6\right.\right.\)