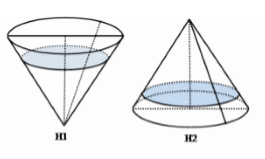
Xét một hình trụ nội tiếp tronh hình nón như hình bên dưới , trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ ; AC, BD cắt nhau tại điểm \(M\in SO.\) Biết rằng tỉ số thể tích của hình trụ và hình nón là \(\frac{4}{9}.\) Tính tỷ số \(\frac{SM}{SO}.\)

Câu hỏi liên quan

• Cho hình nón có độ dài đường sinh bằng 5, bán kính bằng 3. Diện tích toàn phần của hình nón bằng:

• Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là:

• Cho hình vuông ABCD cạnh \(8\,(cm)\). Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là:

ZUNIA12

• Cho hình nón có độ dài đường kính đáy là \(2R\), độ dài đường sinh là \(R\sqrt{17}\) và hình trụ có chiều cao và đường kính đáy đều bằng \(2R\), lồng vào nhau như hình vẽ.

  

  Tính thể tích phần khối trụ không giao với khối nón

• Một người xây nhà phải xây bốn cái cột hình trụ cùng kích cỡ, bán kính đáy các cột là 25cm. Biết rằng tổng thể tích vật liệu (chính là tổng thể tích bốn khối trụ) là 3m³. Chiều cao của mỗi cột là:

• Cho hình chữ nhật ABCD có AB = 3,BC = 4. Gọi V₁,V₂ lần lượt là thể tích của các khối trụ sinh ra khi quay hình chữ nhật quanh trục AB và BC. Khi đó tỉ số  \( \frac{{{V_1}}}{{{V_2}}} \)

• Quay đường cong nào sau đây quanh trục đối xứng của nó ta sẽ được một mặt cầu?

• Một hình trụ có bán kính đáy \(r = 5\,(cm)\), chiều cao \(r = 7\,(cm)\). Diện tích xung quanh của hình trụ này là:

• Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a. Tam giác ABC vuông tại A có \(B C=2 a \sqrt{3}\). Thể tích của hình trụ ngoại tiếp khối lăng trụ này là:

• Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Tính thể tích khối trụ.

• Hình nón (N) có thiết diện qua trục là tam giác đều có cạnh bằng 4. Diện tích toàn phần của (N) bằng

• Một hình trụ có độ dài đường sinh bằng (l ) và bán kính đường tròn đáy bằng (R. ) Diện tích toàn phần của hình trụ đó bằng:

• Quay hình chữ nhật (ABCD ) quanh mỗi cạnh (AB,CD ) thì ta được hai hình trụ có

• Một hình nón có chiều cao bằng \(a\sqrt 3 \) và bán kính đáy bằng a. Diện tích xung quanh của hình nón bằng:

• Trong không gian, cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính diện tích toàn phần S_tp của hình nón khi quay tam giác ABC xung quanh trục AC.

•  Trong không gian, cho tam giác ABC vuông tại A, AB = a và \(AC = \sqrt 3 a\). Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB.

• Một hình trụ có bán kính đáy r =5 cm, chiều cao h=7cm . Diện tích xung quanh của hình trụ này là

• Trong các mệnh đề sau, mệnh đề nào đúng?

• Cho hình nón có bán kính đáy bằng 4a và chiều cao bằng 3a. Diện tích toàn phần của hình nón bằng:

• ho  hình  nón  có  đáy  là  đường  tròn  có  đường  kính 10. Mặt phẳng vuông góc với trục cắt hình nón theo giao  tuyến là một đường tròn như hình vẽ. Thể tích của khối nón có chiều cao bằng 6 là?