Trắc nghiệm Số phức Toán Lớp 12
-
Câu 1:
Cho số phức \(\bar{z}=(1+2 i)(4-3 i)\) . Tọa độ điểm biểu diễn số phức z trên mặt phẳng phức là:
-
Câu 2:
Trong mặt phẳng phức, tìm điểm M biểu diễn số phức \(z=\frac{i^{2017}}{3+4 i}\)
-
Câu 3:
Trong mặt phẳng Oxy, cho \(z_{1}=1-i, z_{2}=3+2 i\) , gọi các điểm M , N lần lượt là điểm biểu diễn số phức \(z_{1}, z_{2}\) , gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?
-
Câu 4:
Cho hình vuông ABCD có tâm H và A, B, C, D, H lần lượt là điểm biểu diễn cho các số phức a , b , c, d , h . Biết \(a=-2+i, h=1+3 i\) và số phức b có phần ảo dương. Khi đó, mô- đun của số phức b là
-
Câu 5:
Cho hai số phức z , w thỏa mãn \(|z+2 w|=3,|2 z+3 w|=6 \text { và }|z+4 w|=7\) . Tính giá trị của biểu thức \(P=z \cdot \bar{w}+\bar{z} \cdot w\)
-
Câu 6:
Cho số phức z thỏa mãn điều kiện \(z+(i-2) z=2+3 i\). Điểm M là điểm biểu diễn số phức z trên mặt phẳng tọa độ Oxy . Tọa độ của điểm M là
-
Câu 7:
Kí hiệu z0 là nghiệm phức có phần ảo dương của phương trình \(4 z^{2}-16 z+17=0\) . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức \(w=i_{20} ?\)
-
Câu 8:
Điểm biểu diễn của số phức z thỏa \((1+i) z=(1-2 i)^{2}\)
-
Câu 9:
Cho số phức z thỏa \((1+i)=14-2 i\) . Điểm biểu diễn của số phức z trong mặt phẳng tọa độ Oxy có tọa độ là:
-
Câu 10:
Cho số phức z thoả mãn \((2-i) z=1+i\)Điểm M biểu diễn số phức z trên mặt phẳng toạ độ Oxy là
-
Câu 11:
Cho số phức \(z_{1}, z_{2}, z_{3}\) thỏa mãn \(\left|z_{1}\right|=\left|z_{2}\right|=\left|z_{3}\right|=1 \text { và } z_{1}+z_{2}+z_{3}=0\) . Tính \(z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\)
-
Câu 12:
Gọi A, B, C lần lượt là các điểm biểu diễn của các số phức \(z_{1}=2, z_{2}=4 i, z_{3}=2+4 i\) trong mặt phẳng tọa độ Oxy. Tính diện tích tam giác ABC
-
Câu 13:
Số nào sau đây là số đối của số phức z , biết z có phần thực dương thỏa mãn \(|z|=2\) và trong mặt phẳng phức thì z có điểm biểu diễn thuộc đường thẳng \(y-\sqrt{3} x=0\)
-
Câu 14:
Cho hai số phức \(z_{1}=1-3 i, z_{2}=-4-6 i\) có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là hai điểm M và N . Gọi z là số phức mà có điểm biểu diễn là trung điểm của đoạn MN. Hỏi z là số phức nào trong các số phức dưới đây?
-
Câu 15:
Cho số phức z thỏa mãn \(i z+2-i=0\) . Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
-
Câu 16:
Cho 3 điểm A , B , C lần lượt biểu diễn cho các số phức \(z_{1}, z_{2}, z_{3}\) . Biết \(\left|z_{1}\right|=\left|z_{2}\right|=\left|z_{3}\right|\) và \({z_{1}}+z_{2}=0\) . Khi đó tam giác ABC là tam giác gì?
-
Câu 17:
Gọi điểm A B , lần lượt biểu diễn các số phức \(z_{1} ; z_{2} ;\left(z_{1} \cdot z_{2} \neq 0\right)\) trên mặt phẳng tọa độ ( \(A, B, C \text { và } A^{\prime}, B^{\prime}, C^{\prime}\) đều không thẳng hàng) và \(z_{1}^{2}+z_{2}^{2}=z_{1} \cdot z_{2}\) . Với O là gốc tọa độ, khẳng định nào sau đây đúng?
-
Câu 18:
Cho số phức z thỏa mãn \((1-2 i)=3+i\). Hỏi điểm biểu diễn của z là điểm nào trong các điểm I, J, K, H ở hình bên?
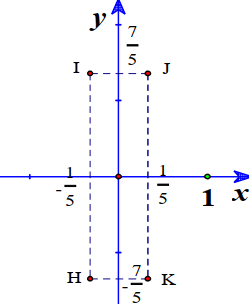
-
Câu 19:
Cho số phức \(z=(1+i)^{8}\) . Tọa độ điểm M biểu diễn z là.
-
Câu 20:
Cho số phức z thỏa mãn \(|z-2+3 i|=|z-2-3 i|\). Biết \(|z-1-2 i|+|z-7-4 i|=6 \sqrt{2}, M(x ; y)\) là điểm biểu diễn số phức z , khi đó x thuộc khoảng
-
Câu 21:
Mặt phẳng phức \(A(-4 ; 1), B(1 ; 3), C(-6 ; 0)\) lần lượt biểu diễn các số phức \(z_{1}, z_{2}, z_{3}\). Trọng tâm G của tam giác ABC biểu diễn số phức nào sau đây?
-
Câu 22:
Kí hiệu z1 là nghiệm phức có phần ảo âm của phương trình \(6 z^{2}-12 z+7=0\) . Trên mặt phẳng tọa độ, tìm điểm biểu diễn của số phức \(w=i z_{1}-\frac{1}{\sqrt{6}}\)
-
Câu 23:
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm môđun của số phức z .
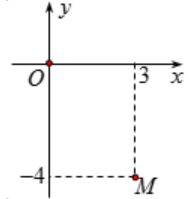
-
Câu 24:
Cho các số phức \(z_{1}, z_{2}, z_{3}, z_{4}\)có các điểm biểu diễn trên mặt phẳng phức lần lượt là A, B, C, D (như hình bên). Tính \(P=\left|z_{1}+z_{2}+z_{3}+z_{4}\right|\)
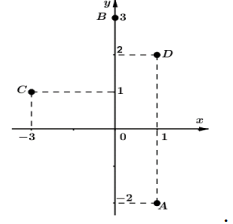
-
Câu 25:
Kí hiệu A , B , C lần lượt là các điểm biểu diễn hình học của các số phức \(z_{1}=1+i ; z_{2}=(1+i)^{2}, z_{3}=a-i, a \in \mathbb{R}\) . Tìm a để tam giác ABC vuông tại B
-
Câu 26:
Cho hai điểm A , B là hai điểm biểu diễn hình học số phức theo thứ tự \(z_{0}, z_{1}\) khác 0 và thỏa mãn đẳng thức \(z_{0}^{2}+z_{1}^{2}=z_{0} z_{1}\) . Hỏi ba điểm O , A , B tạo thành tam giác gì? ( O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
-
Câu 27:
Điểm biểu diễn số phức \(z=\frac{(2-3 i)(4-i)}{3+2 i}\) có tọa độ là
-
Câu 28:
Cho số phức z thỏa mãn \((1+i) z=11-3 i\) . Điểm M biểu diễn cho số phức z trong mặt phẳng tọa độ là
-
Câu 29:
Điểm M trong hình bên là điểm biểu diễn cho số phức
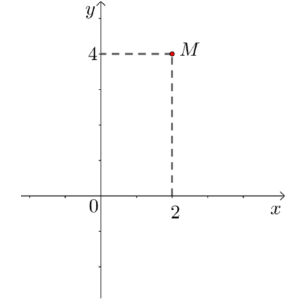
-
Câu 30:
Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình \((1+i) \bar{z}=3-5 i\)
-
Câu 31:
Cho số phức \(z=1-2i\) . Tìm tọa độ biểu diễn của số phức \(\bar z\) trên mặt phẳng tọa độ
-
Câu 32:
Tọa độ điểm biểu diễn hai số phức z và z' lần lượt là tọa độ của hai vectơ \(\vec{u} \text { và } \vec{u}^{\prime}\) . Hãy chọn câu trả lời sai trong các câu sau:
-
Câu 33:
Tìm điểm biểu diễn của số phức \(z=\frac{1}{2-3 i}\) trong mặt phẳng tọa độ Oxy?
-
Câu 34:
Điểm biểu diễn của số phức z là M (1;2). Tọa độ của điểm biểu diễn cho số phức \(w=z-2 \bar{z}\) là
-
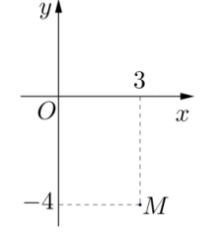
Câu 35:
Điểm M trong hình vẽ trên là điểm biểu diễn cho số phức z. Phần ảo của số phức \((1+i)z\) bằng?
-
Câu 36:
Gọi M , M' theo thứ tự là các điểm biểu diễn số phức \(z \neq 0 \text { và } z^{\prime}=\frac{1+i}{2} z\) . Trong các khẳng định sau, khẳng định nào là đúng?
-
Câu 37:
Cho số phức z thỏa mãn điều kiện \(z-(2+3 i) \bar{z}=1-9 i\) . Số phức \(w=\frac{5}{i z}\) có điểm biểu diễn là điểm nào trong các điểm A , B , C , D ở hình bên?

-
Câu 38:
Cho số phức z thỏa mãn \((1-i) z=2 i\) . Tìm điểm biểu diễn của z trên mặt phẳng tọa độ (Oxy)
-
Câu 39:
Cho tam giác ABC có ba đỉnh A , B , C lần lượt là điểm biểu diễn hình học của các số phức \(z_{1}=2-i, z_{2}=-1+6 i, z_{3}=8+i\) . Số phức z4 có điểm biểu diễn hình học là trọng tâm của tam giác ABC . Mệnh đề nào sau đây là đúng
-
Câu 40:
Gọi z1 là nghiệm phức có phần ảo dương của phương trình \(z^{2}+6 z+13=0\) . Tìm tọa độ điểm M biểu diễn số phức \(w=(i+1) z_{1}\)
-
Câu 41:
Cho A , B , C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức \(z_{1}=1+2 i, z_{2}=-2+5 i, z_{3}=2+4 i\),. Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
-
Câu 42:
Giả sử A , B theo thứ tự là điểm biểu diễn của các số phức \(z_1 ; z_2\) . Khi đó độ dài của véctơ\(\overrightarrow {A B}\) bằng:
-
Câu 43:
Biết số phức z có điểm biểu diễn trên mặt phẳng tọa độ là A(1; -2) .Tìm số phức z
-
Câu 44:
Điểm biểu diễn hình học của số phức \(z=\frac{25}{3+4 i}\) là:
-
Câu 45:
Cho số phức z=-4+2 i . Trong mặt phẳng phức, điểm biểu diễn của z có tọa độ là.
-
Câu 46:
Cho số phức \(z=-2+i\) . Điểm nào dưới đây là điểm biểu diễn của số phức \(w=i z\) trên mặt phẳng tọa độ ?
-
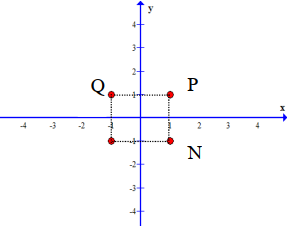
Câu 47:
Cho số phức z thỏa mãn \((1+3 i) z+2 i=-4\) . Điểm nào sau đây biểu diễn cho z trong các điểm M , N , P , Q ở hình bên.
-
Câu 48:
Cho số phức z thỏa mãn \((4-i) z=3-4 i\). Điểm biểu diễn của z là
-
Câu 49:
Tìm điểm M biểu diễn số phức \(z=i-2\)
-
Câu 50:
Cho số phức \(z=2018-2017 i\). Điểm M biểu diễn của số phức liên hợp của z là











