Có tất cả bao nhiêu giá trị nguyên dương của \(m\) không vượt quá 2021 để phương trình \({4^{x - 1}} - m{.2^{x - 2}} + 1 = 0\) có nghiệm?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp:
- Đặt ẩn phụ \(t = {2^{x - 2}} > 0\).
- Cô lập \(m\), đưa phương trình về dạng \(m = g\left( t \right){\mkern 1mu} {\mkern 1mu} \left( {t > 0} \right)\).
- Lập BBT của hàm số \(g\left( t \right)\) khi \(t > 0\).
- Dựa vào BBT tìm giá trị của \(m\) để phương trình có nghiệm.
Cách giải:
Ta có \({4^{x - 1}} - m{.2^{x - 2}} + 1 = 0 \Leftrightarrow 4.{\left( {{2^{x - 2}}} \right)^2} - m{.2^{x - 2}} + 1 = 0\).
Đặt \(t = {2^{x - 2}} > 0\), phương trình đã cho trở thành \(4{t^2} - mt + 1 = 0 \Leftrightarrow m = \dfrac{{4{t^2} + 1}}{t} = g\left( t \right){\mkern 1mu} {\mkern 1mu} \left( {t > 0} \right)\).
Xét hàm số \(g\left( t \right) = \dfrac{{4{t^2} + 1}}{t} = 4t + \dfrac{1}{t}\) có \(g'\left( t \right) = 4 - \dfrac{1}{{{t^2}}} = 0 \Leftrightarrow t = \dfrac{1}{2}\).
BBT:
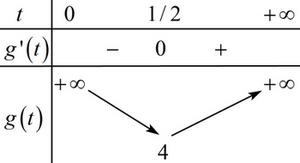
Dựa vào BBT ta thấy phương trình có nghiệm \(t > 0 \Leftrightarrow m \ge 4\).
Kết hợp điều kiện \(\left\{ {\begin{array}{*{20}{l}}{m \in {\mathbb{Z}^ + }}\\{m \le 2021}\end{array}} \right. \Rightarrow m \in \left\{ {4;5;6;...;2020;2021} \right\}\).
Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn B.
Đề thi giữa HK2 môn Toán 12 năm 2023-2024
Trường THPT Lạc Long Quân