Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \({x^3} + {x^2} + x = m{\left( {{x^2} + 1} \right)^2}\) có nghiệm thuộc đoạn [0;1].
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\({x^3} + {x^2} + x = m{\left( {{x^2} + 1} \right)^2} \)
\(\Rightarrow m = \frac{{{x^3} + {x^2} + x}}{{{{\left( {{x^2} + 1} \right)}^2}}} \ge 0\)
Xét hàm số \(y = \frac{{{x^3} + {x^2} + x}}{{{{\left( {{x^2} + 1} \right)}^2}}}\) liên tục trên đoaạn [0;1].
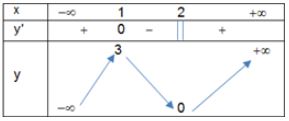
\(\begin{array}{l} y' = \frac{{ - {x^4} - 2{x^3} + 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^3}}} = \frac{{ - (x - 1){{(x + 1)}^3}}}{{{{({x^2} + 1)}^3}}}\\ y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\,\, \in \left[ {0;1} \right]\\ x = - 1\,\, \notin \left[ {0;1} \right] \end{array} \right.. \end{array}\)
Ta có: \(f(0) = 1;\,\,f(1) = \frac{3}{4}.\)
Kết luận: Để phương trình có nghiệm thuộc [0;1] thì \(0\leq m \leq \frac{3}{4}\).
Đề thi giữa HK1 môn Toán 12 năm 2022-2023
Trường THPT Trần Hưng Đạo