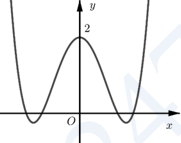
Cho hàm số bậc 4 \(y=f(x)\) có đồ thị hàm số \(y={f}'\left( x \right)\) như hình. Hàm số \(g\left( x \right)=4f\left( {{x}^{2}}-4 \right)+{{x}^{4}}-8{{x}^{2}}\) có bao nhiêu điểm cực tiểu?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(g\left( x \right)=4f\left( {{x}^{2}}-4 \right)+{{x}^{4}}-8{{x}^{2}}\)\( \Rightarrow {g}'\left( x \right)=8x{f}'\left( {{x}^{2}}-4 \right)+4{{x}^{3}}-16x\)
Ta có \({g}'\left( x \right)=0\)
\(\begin{array}{l} \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {f'\left( {{x^2} - 4} \right) + \frac{1}{2}\left( {{x^2} - 4} \right) = 0} \end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {f'\left( {{x^2} - 4} \right) = - \frac{1}{2}\left( {{x^2} - 4} \right)} \end{array}} \right. \end{array}\)
Xét phương trình \({f}'\left( {{x}^{2}}-4 \right)=-\frac{1}{2}\left( {{x}^{2}}-4 \right)\).
Đặt \(t={{x}^{2}}-4\), khi đó \({f}'\left( {{x}^{2}}-4 \right)=-\frac{1}{2}\left( {{x}^{2}}-4 \right)\Leftrightarrow {f}'\left( t \right)=-\frac{1}{2}t\).
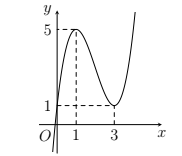
Phát họa đồ thị hàm số \(y={f}'\left( t \right)\) và \(y=\frac{1}{2}t\) trên cùng một hệ trục tọa độ:
Khi đó
\({f}'\left( t \right)=-\frac{1}{2}t\Leftrightarrow \left[ \begin{matrix} t=-1 \\ t=0 \\ t=4 \\ \end{matrix} \right.\)
Khi đó
\(\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {f'\left( {{x^2} - 4} \right) = - \frac{1}{2}\left( {{x^2} - 4} \right)} \end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {{x^2} - 4 = - 1}\\ {{x^2} - 4 = 0}\\ {{x^2} - 4 = 4} \end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = \pm \sqrt 3 }\\ {x = 2}\\ {x = \pm 2\sqrt 2 } \end{array}} \right. \end{array}\)
Vậy \(g\left( x \right)=4f\left( {{x}^{2}}-4 \right)+{{x}^{4}}-8{{x}^{2}}\) có \(7\) điểm cục trị, mà \(\underset{x\to \infty }{\mathop{\lim }}\,g\left( x \right)=+\infty \) nên hàm số \(g\left( x \right)\) có \(4\) điểm cực tiểu.
Chọn A
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Tân Phong
.PNG)
.PNG)
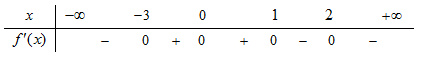
.PNG)
.PNG)











