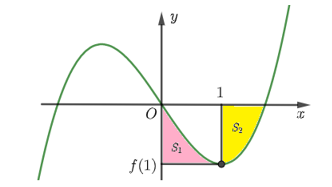
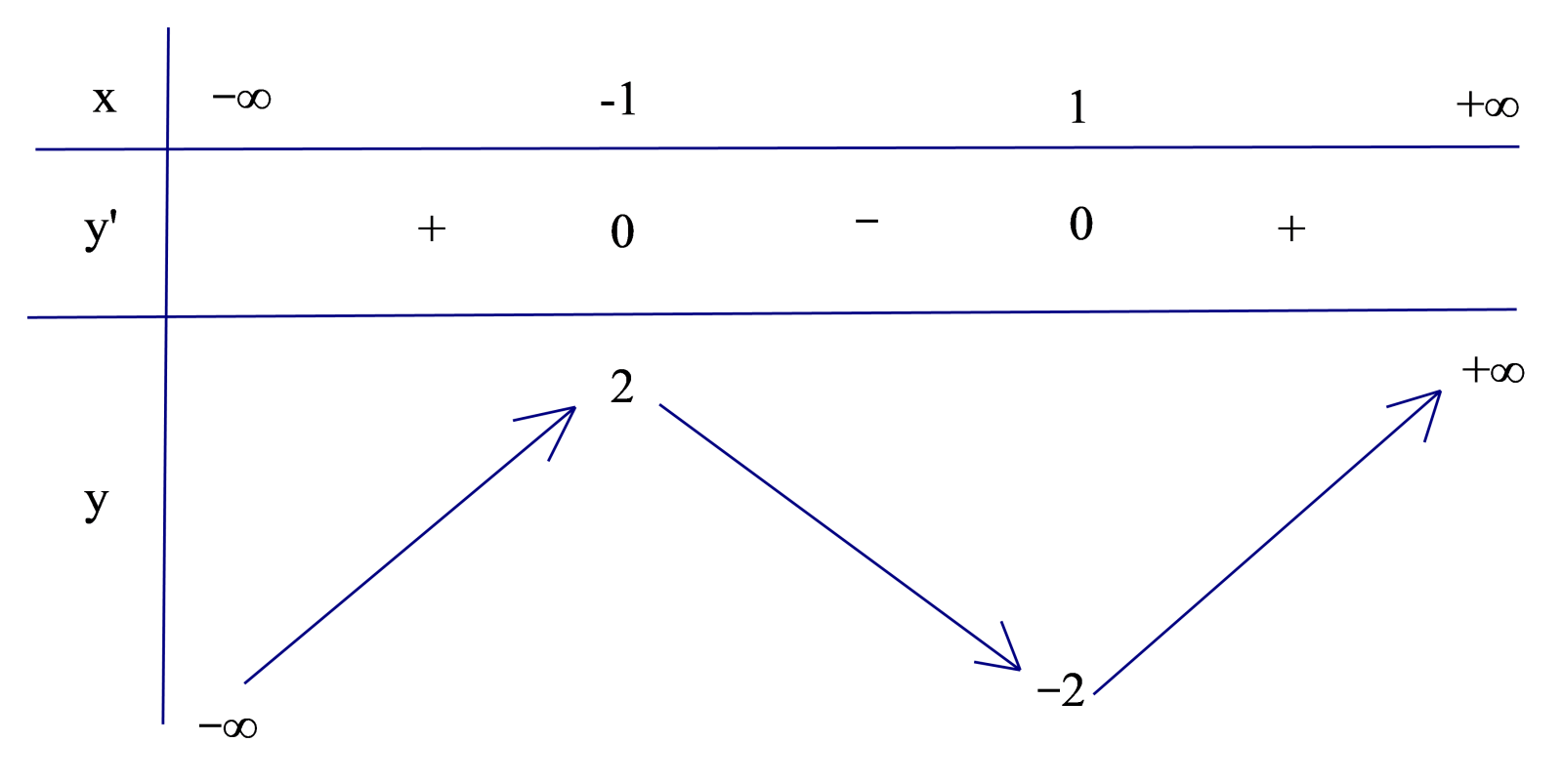
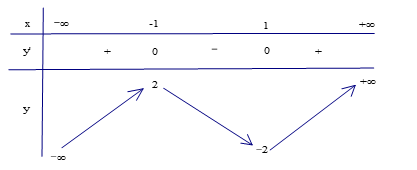
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình vẽ, biết \(f\left( x \right)\) đạt cực tiểu tại điểm \(x=1\) và thỏa mãn \(\left[ f\left( x \right)+1 \right]\) và \(\left[ f\left( x \right)-1 \right]\) lần lượt chia hết cho \({{\left( x-1 \right)}^{2}}\) và \({{\left( x+1 \right)}^{2}}\). Gọi \({{S}_{1}},{{S}_{2}}\) lần lượt là diện tích như trong hình bên. Tính \(2{{S}_{2}}+8{{S}_{1}}\).

Câu hỏi liên quan

• Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD.\) Cặp đường thẳng nào sau đây cắt nhau?

• Cho hai tích phân \(\int\limits_{-2}^{5}{f\left( x \right)\text{d}}x=8\) và \(\int\limits_{5}^{-2}{g\left( x \right)\text{d}}x=3\). Tính \(I=\int\limits_{-2}^{5}{\left[ f\left( x \right)-4g\left( x \right)-1 \right]\text{d}}x\)

• Hàm số nào dưới đây có bảng biến thiên như sau:

   

ZUNIA12

• Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\), \(\left( a,b,c\in R \right)\) có đồ thị là đường cong như hình bên. Điểm cực tiểu của hàm số đã cho là:

  

• Cho tam giác \(ABC\)có trọng tâm \(G\). Mệnh đề nào sau đây là mệnh đề SAI?

• Tập nghiệm của bất phương trình \({{3}^{{{x}^{2}}-13}}<27\) là

• Tìm tập nghiệm \(S\) của bất phương trình \({{5}^{x+1}}-\frac{1}{5}>0\).

• Cho hình nón đỉnh\(S\), đáy là đường tròn \(\left( O;\,5 \right)\).Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm \(A\) và \(B\) sao cho \(SA=AB=8\). Tính khoảng cách từ \(O\) đến \(\left( SAB \right)\).

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA=a\) và \(SA\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABCD\) bằng

• Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\text{ }\!\![\!\!\text{ }-1;\,2]\) và \(f\left( -1 \right)=2023,\,f\left( 2 \right)=-1. \)Tích phân \(\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}\)bằng:

• Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng \(A{B}'\) và \(C{C}'\) bằng

  

• Hàm số nào dưới đây có bảng biến thiên như sau:

  

• Gọi \({{z}_{1}}\) là nghiệm phức có phần ảo âm của phương trình \({{z}^{2}}-2z+5=0\). Tọa độ điểm biểu diễn số phức \(\frac{7-4i}{{{z}_{1}}}\) trên mặt phẳng phức là

• Nghiệm của phương trình \({{\log }_{3}}\left( 2x+1 \right)=1+{{\log }_{3}}\left( x-1 \right)\) là

• Khẳng định nào sau đây đúng?

• Số giao điểm của đồ thị \((C):y={{x}^{3}}-3{{x}^{2}}+2x+1\) và đường thẳng \(y=1\) là

• Đạo hàm của hàm số \(y={{8}^{x}}\) là

• Cho \(I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+{{\left( x+\ln x \right)}^{2}}+x}{{{x}^{2}}{{\left( x+\ln x \right)}^{2}}}\text{d}x}=\frac{a}{2}-\frac{1}{b+\ln c}\) với \(a\), \(b\), \(c\) là các số nguyên dương. Khẳng định nào sau đây đúng ?

• Trong không gian \(Oxyz\), phương trình mặt phẳng \(\left( P \right)\) song song và cách đều hai đường thẳng \({{d}_{1}}:\frac{x-2}{-1}=\frac{y}{1}=\frac{z}{1}\) và \({{d}_{2}}:\frac{x}{2}=\frac{y-1}{-1}=\frac{z-2}{-1}\) là

• Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy hai điểm \(A,B\) phân biệt thuộc \(a\) và hai điểm \(C,D\) phân biệt thuộc \(b\). Khi đó hai đường thẳng \(A\text{D}\) và \(BC\) ở vị trí