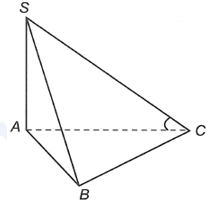
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông cân tại \(C\) và \(SA\) vuông góc với mặt phẳng đáy. Cho \(SC=a\), mặt phẳng \(\left( SBC \right)\) tạo với mặt đáy một góc \(\alpha \). Thể tích khối chóp \(S.ABC\) đạt giá trị lớn nhất là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn B
Ta có \(\widehat{\left( \left( SBC \right),\left( ABC \right) \right)}=\left( \widehat{SC,AC} \right)=\widehat{SCA}=\alpha \)
Xét \(\Delta SAC\) vuông tại \(A\) có
\(\left\{ \begin{align} & SA=SC.\sin \alpha =a\sin \alpha \\ & AC=SC.\cos \alpha =a\cos \alpha \\ \end{align} \right.\)
\(\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}{{S}_{\Delta ABC}}.SA\)\( =\frac{1}{3}.\left( \frac{1}{2}A{{C}^{2}} \right).SA\)
\(=\frac{1}{6}.{{\left( a\cos \alpha \right)}^{2}}.a\sin \alpha \)\( =\frac{{{a}^{3}}}{6}{{\cos }^{2}}\alpha .\sin \alpha .\)
\({{V}_{S.ABC}}\) đạt giá trị lớn nhất khi và chỉ khi biểu thức
\(P={{\cos }^{2}}\alpha .\sin \alpha .=\left( 1-{{\sin }^{2}}\alpha \right).\sin \alpha \) đạt giá trị lớn nhất.
Đặt \(t=\sin \alpha \).
Vì \(0<\alpha <90{}^\circ \) nên \(0<\sin \alpha <1\)
\(\Rightarrow 0<t<1\)
Ta có \(P=f\left( t \right)=\left( 1-{{t}^{2}} \right)t=-{{t}^{3}}+t\) xác định và liên tục trên \(\left( 0;1 \right)\).
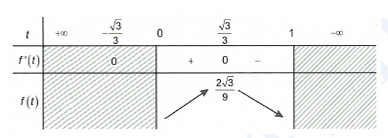
\({f}'\left( t \right)=-3{{t}^{2}}+1\)\( \Rightarrow {f}'\left( t \right)=0\)
\(\Leftrightarrow \left[ \begin{align} & t=\frac{\sqrt{3}}{3}\text{ (nhan)} \\ & t=-\frac{\sqrt{3}}{3}\text{ (loai) } \\ \end{align} \right.\)
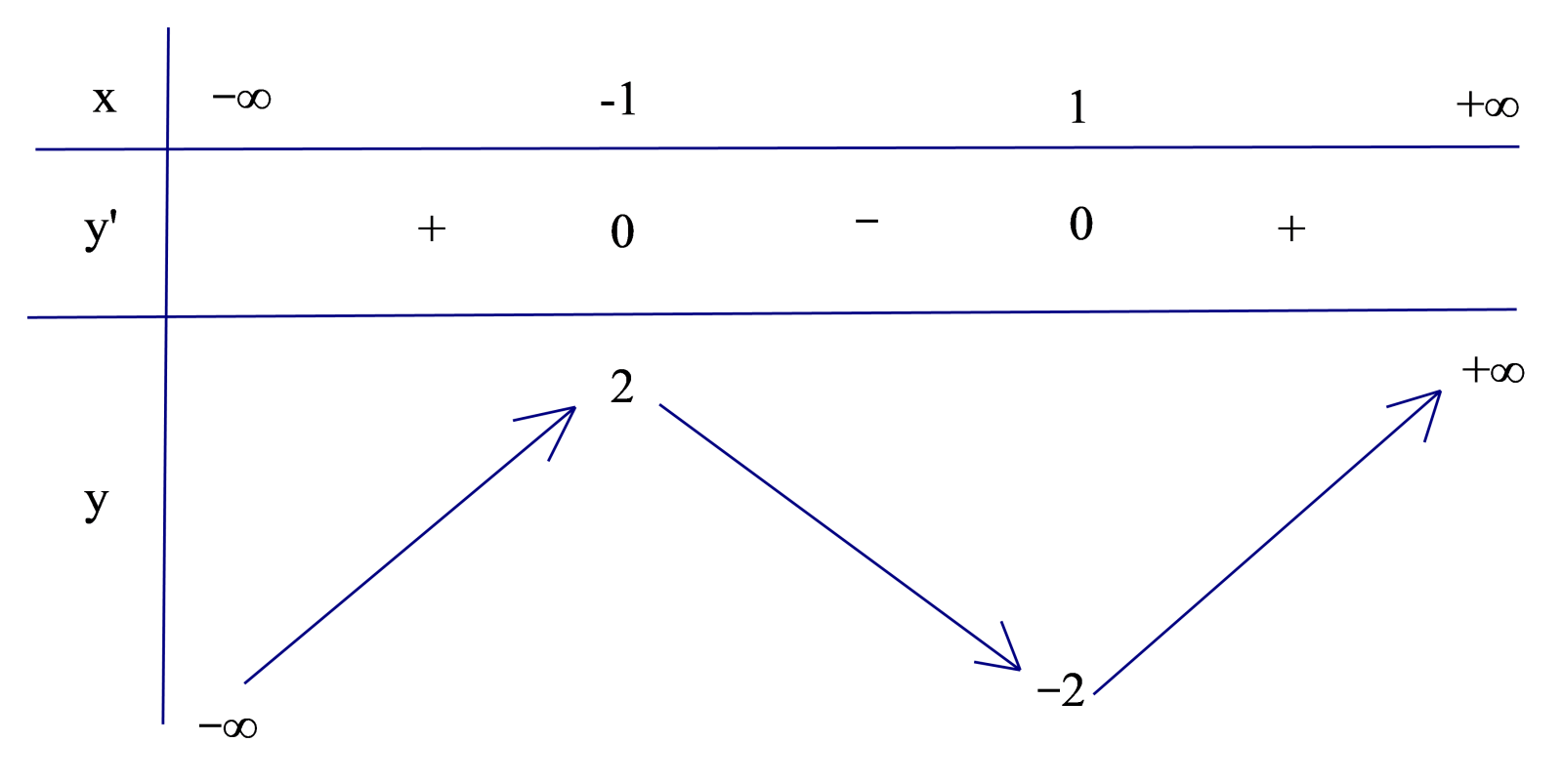
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có \(\underset{\left( 0;1 \right)}{\mathop{\max f\left( t \right)}}\,=\frac{2\sqrt{3}}{9}\) khi \(t=\frac{\sqrt{3}}{3}\).
Vậy \(\max {{V}_{S.ABC}}=\frac{{{a}^{3}}}{6}.{{P}_{\max }}\)\( =\frac{{{a}^{3}}}{6}.\frac{2\sqrt{3}}{9}=\frac{{{a}^{3}}\sqrt{3}}{27}\) khi và chỉ khi \(\sin \alpha =\frac{\sqrt{3}}{3}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Phú Lâm
Câu hỏi liên quan
-
Cho hàm số \(f\left( x \right)\) có đạo hàm\(f'\left( x \right)=x\left( x-1 \right){{\left( x+4 \right)}^{2023}},\,\forall x\in \mathbb{R}\) . Số điểm cực trị của hàm số đã cho là
-
Thể tích của khối lăng trụ có diện tích đáy \(S=2{{a}^{2}}\), chiều cao \(h=6a\) là:
-
Tìm tập nghiệm \(S\) của bất phương trình \({{5}^{x+1}}-\frac{1}{5}>0\).
-
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ -1;1 \right\}\), thỏa mãn \(f'\left( x \right)=\frac{2}{{{x}^{2}}-1};\ f\left( -3 \right)+f\left( 3 \right)=2\ln 2\) và \(f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=0\). Giá trị của biểu thức \(P=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)\) là:
-
Cho hai số phức \({{z}_{1}}=2+i,{{z}_{2}}=1-2i.\) Môđun của số phức \(w=\frac{z_{1}^{2022}}{z_{2}^{2023}}\) là
-
Trong không gian \(Oxyz\), mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=25\) có tọa độ tâm \(I\) và bán kính \(R\) là
-
Cho hai tích phân \(\int\limits_{-2}^{5}{f\left( x \right)\text{d}}x=8\) và \(\int\limits_{5}^{-2}{g\left( x \right)\text{d}}x=3\). Tính \(I=\int\limits_{-2}^{5}{\left[ f\left( x \right)-4g\left( x \right)-1 \right]\text{d}}x\)
-
Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\), \(\left( a,b,c\in R \right)\) có đồ thị là đường cong như hình bên. Điểm cực tiểu của hàm số đã cho là:
-
Hàm số nào dưới đây có bảng biến thiên như sau:
-
Trong các mệnh đề sau, mệnh đề nào sai?
-
Cho hình chóp \(S.ABC\)có \(SA=a\) và \(SA\) vuông góc với đáy. Biết đáy là tam giác vuông cân tại \(A\) và \(BC=a\sqrt{2}\). Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( SBC \right)\).
-
Phương trình tiếp tuyến của đường cong \(y={{x}^{3}}+3{{x}^{2}}-2\) tại điểm có hoành độ \({{x}_{0}}=1\) là
-
Khẳng định nào sau đây đúng?
-
Hàm số nào dưới đây có bảng biến thiên như sau:
-
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình vẽ, biết \(f\left( x \right)\) đạt cực tiểu tại điểm \(x=1\) và thỏa mãn \(\left[ f\left( x \right)+1 \right]\) và \(\left[ f\left( x \right)-1 \right]\) lần lượt chia hết cho \({{\left( x-1 \right)}^{2}}\) và \({{\left( x+1 \right)}^{2}}\). Gọi \({{S}_{1}},{{S}_{2}}\) lần lượt là diện tích như trong hình bên. Tính \(2{{S}_{2}}+8{{S}_{1}}\).
-
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng \(A{B}'\) và \(C{C}'\) bằng
-
Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng \(a\) có diện tích bằng \(8{{a}^{2}}\sqrt{3}\). Thể tích của khối trụ là
-
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol \(y=\sqrt{3}{{x}^{2}}\), cung tròn có phương trình \(y=\sqrt{4-{{x}^{2}}}\) (với \(0\le x\le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) là
-
Gọi \({{z}_{1}}\) là nghiệm phức có phần ảo âm của phương trình \({{z}^{2}}-2z+5=0\). Tọa độ điểm biểu diễn số phức \(\frac{7-4i}{{{z}_{1}}}\) trên mặt phẳng phức là
-
Nghiệm của phương trình \({{\log }_{3}}\left( 2x+1 \right)=1+{{\log }_{3}}\left( x-1 \right)\) là
