Cho hàm số bậc bốn \(y=f(x)\) có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g(x)=f({{x}^{3}}-3{{x}^{2}})\) là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(g(x)=f({{x}^{3}}-3{{x}^{2}})\Rightarrow g'(x)=(3{{x}^{2}}-6x).f'({{x}^{3}}-3{{x}^{2}})\).
\(g'(x)=0\Leftrightarrow \left[ \begin{matrix} 3{{x}^{2}}-6x=0 \\ f'({{x}^{3}}-3{{x}^{2}})=0 \\ \end{matrix} \right.\\ \Leftrightarrow \left[ \begin{matrix} x=0 \\ x=2 \\ {{x}^{3}}-3{{x}^{2}}=a\,(a<-4) \\ {{x}^{3}}-3{{x}^{2}}=b\,(-4<b<0) \\ {{x}^{3}}-3{{x}^{2}}=c\,(c>0) \\ \end{matrix} \right.\)
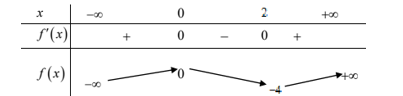
Ta có bảng biến thiên của hàm số \(y={{x}^{3}}-3{{x}^{2}}\).
Dựa vào bảng biến thiên ta có: \({{x}^{3}}-3{{x}^{2}}=a\,(a < -4)\) có 1 nghiệm.
\({{x}^{3}}-3{{x}^{2}}=b\,(-4 < b < 0)\) có 3 nghiệm.
\({{x}^{3}}-3{{x}^{2}}=c\,(c > 0)\) có 1 nghiệm.
Vậy số điểm cực trị của hàm số \(g(x)=f({{x}^{3}}-3{{x}^{2}})\) là 7.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Võ Thị Sáu
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)











