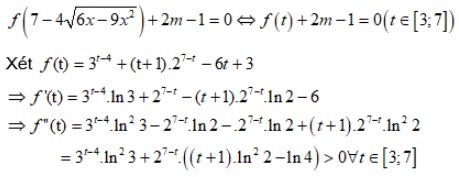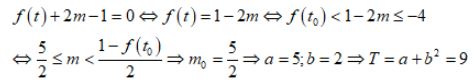Cho hàm số \(f\left( x \right) = {3^{x - 4}} + \left( {x + 1} \right){.2^{7 - x}} - 6x + 3\). Giả sử \({m_0} = \frac{a}{b}\) (\(a,b \in Z,\frac{a}{b}\) là phân số tối giản) là giá trị nhỏ nhất của tham số thực m sao cho phương trình \(f\left( {7 - 4\sqrt {6x - 9{x^2}} } \right) + 2m - 1 = 0\) có số nghiệm nhiều nhất. Tính giá trị của biểu thức \(P = a + {b^2}\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt
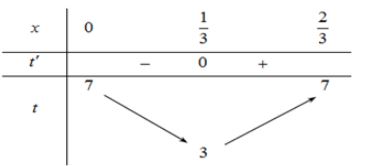
\(\begin{array}{l} t = 7 - 4\sqrt {6x - 9{x^2}} \left( {x \in \left[ {0;\frac{2}{3}} \right]} \right)\\ \Rightarrow t' = \frac{{36x - 12}}{{\sqrt {6x - 9{x^2}} }}\\ \Rightarrow t' = 0\\ \Rightarrow x = \frac{1}{3} \end{array}\)
Bảng biến thiên
Ta có \(t \in \left[ {3;7} \right]\) và t = 3 có 1 nghiệm; \(t \in \left( {3;7} \right]\) có hai nghiệm.
Vậy f’(t)=0 có nhiều nhất 1 nghiệm trên đoạn [3;7]
Vì f’(6).f’(7)<0 suy ra f’(t)=0 có nghiệm \(t_0 \in (6;7)\)
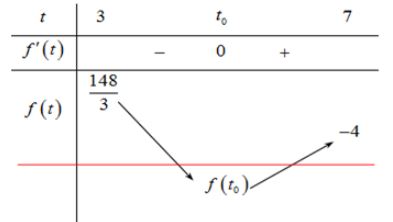
Bảng biến thiên
Ta thấy khi \(f(t) \in [f(t_0);-4]\) thì phương trình có nghiệm nhiều nhất
Đề thi thử THPT QG môn Toán năm 2019
Trường THPT Chuyên Hưng Yên lần 3