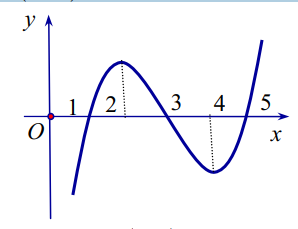
Cho hàm số y=f(x). Đồ thị hàm số y =f'(x) như hình vẽ. Cho bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) (m là tham số thực). Điều kiện cần và đủ để bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) đúng với mọi \(x \in[-\sqrt{3} ; \sqrt{3}]\) là:
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saita có: \(3 f(x) \geq x^{3}-3 x+m \Leftrightarrow 3 f(x)-x^{3}+3 x \geq m\)
Đặt \(g(x)=3 f(x)-x^{3}+3 x\)
\(g^{\prime}(x)=3 f^{\prime}(x)-3 x^{2}+3\)
\(g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=x^{2}-1\)
Nghiệm của phương trình \(g^{\prime}(x)=0\) là hoành độ giao điểm của đồ thị hàm số \(y=f^{\prime}(x)\) và parabol \(y=x^{2}-1\)
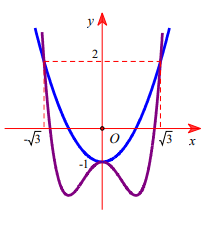
Dựa vào đồ thị hàm số :
\(f^{\prime}(x)=x^{2}-1 \Leftrightarrow\left[\begin{array}{l} x=-\sqrt{3} \\ x=0 \\ x=\sqrt{3} \end{array}\right.\)
Bảng biến thiên:
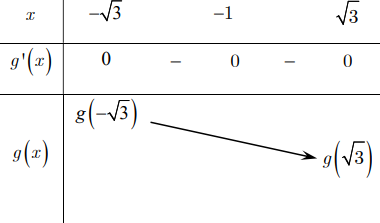
Để bất phương trình nghiệm đúng với mọi \(x \in[-\sqrt{3} ; \sqrt{3}]\)
thì \(m \leq \min\limits _{[-\sqrt{3} ; \sqrt{3}]} g(x)=g(\sqrt{3})=3 f(\sqrt{3})\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Bến Tre lần 1