Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữa nhật, \(AB=2,\,AD=2\sqrt{3}\), tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc đáy, k/c giữa 2 đường thẳng \(AB\) và \(SC\)bằng \(3\). Tính thể tích của khối chóp \(S.ABCD\) bằng?

Câu hỏi liên quan

• Hàm số nào sau đây có đồ thị là đường cong như hình?

  

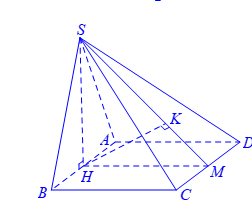
• Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB=1,AD=AA'=\sqrt{3}\). Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và \(BC\). Góc giữa 2 đường thẳng \(MN\) và \(AC\) bằng?

• Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(a\) là số thực dương. Khẳng định nào đúng? 

ZUNIA12

• Cho các số phức \(w,\,z\) thỏa mãn \(\left| w+i \right|=\frac{3\sqrt{5}}{5}\) và \(5w=\left( 2+i \right)\left( z-4 \right)\). GTLN của biểu thức \(P=\left| z-1-2i \right|+\left| z-5-2i \right|\) bằng?

• Trong không gian \(Oxyz\), cho mặt cầu \((S):{{(x+1)}^{2}}+{{(y-1)}^{2}}+{{z}^{2}}=4\) và hai điểm \(A(1\,;\,2\,;\,4)\), \(B(0\,;\,0\,;\,1)\). Mặt phẳng \((P):ax+by+cz+3=0\) \((a,b,c\in \mathbb{R})\)  đi qua \(A,B\) và cắt \((S)\) theo giao tuyến là 1 đường tròn có bán kính nhỏ nhất. Giá trị của \(a+b+c\) bằng?

• Môđun của số phức sau \(z=4-3i\) bằng?

• Tính số cách xếp 4 người thành một hàng ngang là?

• Cho CSC \(\left( {{u}_{n}} \right)\)biết \({{u}_{1}}=5,\,{{u}_{2}}=8\). Giá trị của \({{u}_{4}}\) bằng?

• Cho \(\left( H \right)\) là hình phẳng giới hạn bởi ĐTHS \(y={{x}^{2}}-4x+4\), trục hoành và trục tung. Đường thẳng \(d\) qua \(A\left( 0\,;\,4 \right)\) và có hệ số góc \(k\,\,\left( k\in \mathbb{R} \right)\) chia hình \(\left( H \right)\) thành 2 phần có diện tích bằng nhau. Giá trị của \(k\) bằng?

• Tính thể tích của khối trụ có chiều cao \(h=2\) và bán kính đáy \(r=3\)?

• Số nghiệm nguyên của bất phương trình sau \({{\log }_{\frac{1}{4}}}\left( x-1 \right)+{{\log }_{4}}\left( 14-2x \right)\ge 0\) là?

• Cho số phức \(z={{\left( 1+2i \right)}^{2}}\). Gía trị của số phức \(\frac{z}{i}\) bằng?

• Cho hàm số \(y=f\left( x \right)\) có đồ thị là đường cong như hình:

  

  Hàm số đã cho đồng biến trên khoảng nào?

• Họ nguyên hàm của của hàm số sau đây \(f\left( x \right)={{x}^{2}}-3x\) là?

• TXĐ của hàm số \(y={{x}^{\sqrt{5}}}\) là?

• GTLN của hàm số \(f\left( x \right)=2{{x}^{3}}-6x\) trên đoạn \(\left[ 0;2 \right]\) bằng?

• Cho hàm số có bảng biến thiên như sau:

  

  Hàm số đã cho đạt CĐ tại?

• Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh đều bằng \(2\) (tham khảo hình). K/c từ \(B\) đến mặt phẳng \(\left( AC{C}'{A}' \right)\) bằng?

  

• Hàm số \(y=\frac{{{x}^{3}}}{3}-2{{x}^{2}}+3x+1\) nghịch biến trên khoảng nào?

• Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( 3;\,-1;\,2 \right)\) và có VTCP \(\overrightarrow{u}=\left( 4;\,5;\,-7 \right)\) có phương trình là?