Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Minh Đức
-
Câu 1:
Tính số cách xếp 4 người thành một hàng ngang là?
-
Câu 2:
TXĐ của hàm số \(y={{x}^{\sqrt{5}}}\) là?
-
Câu 3:
Trong không gian \(Oxyz\), cho mặt phẳng \((P):3x+y-2z+1=0\). Vectơ nào là một vectơ pháp tuyến của \((P)\)?
-
Câu 4:
Cho hàm số \(y=f(x)\) có đồ thị là đường cong như hình:
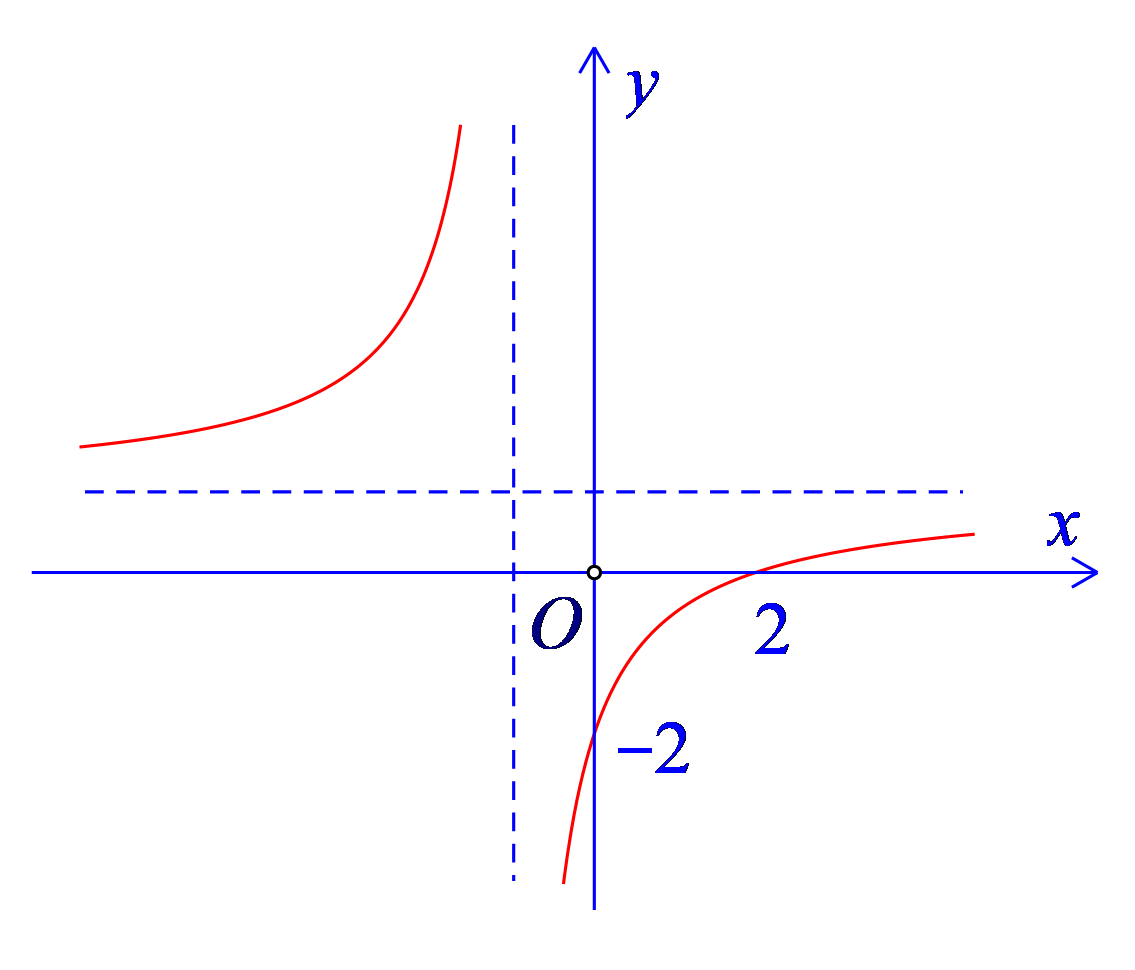
Đồ thị hàm số đã cho cắt trục hoành tại điểm nào?
-
Câu 5:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(a\) là số thực dương. Khẳng định nào đúng?
-
Câu 6:
Môđun của số phức sau \(z=4-3i\) bằng?
-
Câu 7:
Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( 3;\,-1;\,2 \right)\) và có VTCP \(\overrightarrow{u}=\left( 4;\,5;\,-7 \right)\) có phương trình là?
-
Câu 8:
Trong không gian \(Oxyz\), cho 2 véctơ \(\vec{a}=\left( 2\,;\,3\,;\,2 \right)\) và \(\vec{b}=\left( 1\,;\,1\,;\,-1 \right)\). Véctơ \(\vec{a}-\vec{b}\) có toạ độ là?
-
Câu 9:
Tính giá trị của \(\int\limits_{2}^{5}{\frac{1}{x}\text{d}x}\) bằng?
-
Câu 10:
Tính thể tích của khối cầu có bán kính \(R\)?
-
Câu 11:
Cho khối lăng trụ có diện tích đáy bằng \(B\) và chiều cao bằng \(h\). Thể tích \(V\) của khối lăng trụ đã cho được tính theo công thức nào?
-
Câu 12:
Tính thể tích của khối trụ có chiều cao \(h=2\) và bán kính đáy \(r=3\)?
-
Câu 13:
Trong không gian \(Oxyz\), điểm nào thuộc đường thẳng \(d:\frac{x-1}{2}=\frac{y}{1}=\frac{z+1}{2}?\)
-
Câu 14:
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(k\) là một số thực khác 0. Khẳng định nàođúng?
-
Câu 15:
Nghiệm của phương trình sau \({{3}^{x}}=7\) là?
-
Câu 16:
Cho hàm số \(y=f\left( x \right)\) có đồ thị là đường cong như hình:
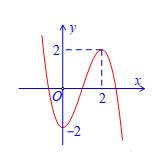
Hàm số đã cho đồng biến trên khoảng nào?
-
Câu 17:
Cho 2 số phức sau \({{z}_{1}}=2+3i\) và \({{z}_{2}}=3-2i\). Số phức \({{z}_{1}}.{{z}_{2}}\) bằng?
-
Câu 18:
Với \(a\) là số thực dương, giá trị của \(\log {{a}^{10}}\) bằng?
-
Câu 19:
Hàm số nào sau đây có đồ thị là đường cong như hình?
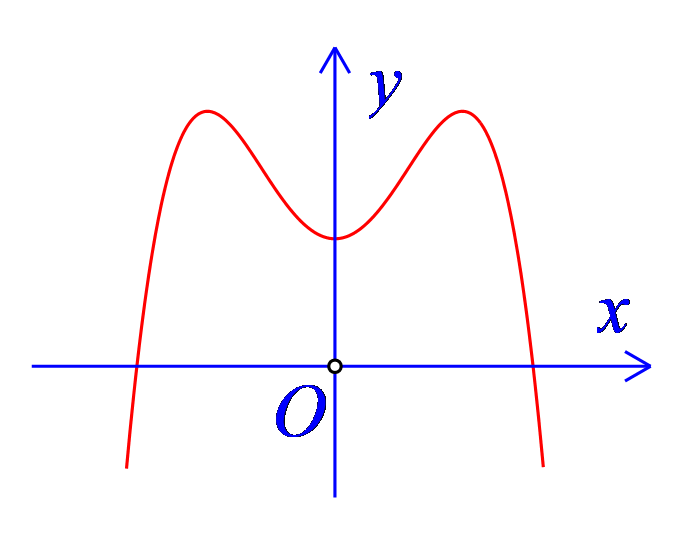
-
Câu 20:
Điểm \(M\) trong hình bên dưới biểu diễn số phức nào?

-
Câu 21:
Cho hàm số có bảng biến thiên như sau:

Hàm số đã cho đạt CĐ tại?
-
Câu 22:
Tiệm cận đứng của ĐTHS \(y=\frac{2x-4}{x+1}\) là đường thẳng có phương trình?
-
Câu 23:
Trong không gian \(Oxyz\), cho mặt cầu tâm \(I\left( 1\,;\,0\,;\,-2 \right)\) và bán kính \(R=4\) có phương trình là?
-
Câu 24:
Cho khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\). Thể tích V của khối chóp đã cho bằng?
-
Câu 25:
Số nghiệm nguyên của bất phương trình sau \({{\log }_{\frac{1}{4}}}\left( x-1 \right)+{{\log }_{4}}\left( 14-2x \right)\ge 0\) là?
-
Câu 26:
Cho HS \(f\left( x \right)\) liên tục trên đoạn \(\left[ 0\,;\,2 \right]\) và thỏa mãn \(\int\limits_{0}^{2}{f\left( x \right)\text{d}x}=6\). Giá trị của tích phân \(\int\limits_{0}^{\frac{\pi }{2}}{f\left( 2\sin x \right)\cos x\text{d}x\,}\) bằng?
-
Câu 27:
Cho biết \({{\log }_{a}}5=3\), khi đó giá trị của \({{\log }_{{{a}^{2}}}}\left( 5{{a}^{3}} \right)\) bằng?
-
Câu 28:
Hàm số \(y=\frac{{{x}^{3}}}{3}-2{{x}^{2}}+3x+1\) nghịch biến trên khoảng nào?
-
Câu 29:
GTLN của hàm số \(f\left( x \right)=2{{x}^{3}}-6x\) trên đoạn \(\left[ 0;2 \right]\) bằng?
-
Câu 30:
Họ nguyên hàm của của hàm số sau đây \(f\left( x \right)={{x}^{2}}-3x\) là?
-
Câu 31:
Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh đều bằng \(2\) (tham khảo hình). K/c từ \(B\) đến mặt phẳng \(\left( AC{C}'{A}' \right)\) bằng?
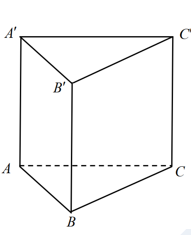
-
Câu 32:
Cho CSC \(\left( {{u}_{n}} \right)\)biết \({{u}_{1}}=5,\,{{u}_{2}}=8\). Giá trị của \({{u}_{4}}\) bằng?
-
Câu 33:
Cho hàm số sau \(y=f\left( x \right)\) có đạo hàm \({f}'\left( x \right)=x\left( x-1 \right)\left( x+3 \right)\). Hàm số đạt CĐ tại điểm?
-
Câu 34:
Cho hàm số sau \(f(x)\)có đạo hàm \({f}'(x)=\frac{1}{\sqrt{1-3x}},\forall x\in \left( -\infty ;\frac{1}{3} \right)\) và \(f(-1)=\frac{2}{3}\). Biết \(F(x)\) là nguyên hàm của \(f(x)\) thỏa mãn \(F(-1)=0\). Giá trị của \(F\left( \frac{1}{4} \right)\) bằng?
-
Câu 35:
Trên tập hợp số phức, biết \({{z}_{0}}=3-2i\) là một nghiệm của phương trình \({{z}^{2}}+az+b=0\)(với \(a,\,\,b\in \mathbb{R}\)). Tính giá trị của \(a+b\) bằng?
-
Câu 36:
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB=1,AD=AA'=\sqrt{3}\). Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và \(BC\). Góc giữa 2 đường thẳng \(MN\) và \(AC\) bằng?
-
Câu 37:
Một hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng. Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Xác suất để trong 3 quả cầu lấy được có ít nhất 1 quả màu đỏ?
-
Câu 38:
Cho hàm số bậc 3 \(y=f\left( x \right)\) có đồ thị là đường cong như hình:
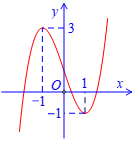
Số nghiệm của phương trình \(f\left[ f\left( x \right) \right]=0\) là?
-
Câu 39:
Tìm TXĐ của hàm số \(y={{\log }_{3}}\left( {{x}^{2}}-1 \right)\) là?
-
Câu 40:
Cho số phức \(z={{\left( 1+2i \right)}^{2}}\). Gía trị của số phức \(\frac{z}{i}\) bằng?
-
Câu 41:
Hỏi tất cả có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {{9}^{x}}-{{10.3}^{x+2}}+729 \right)\sqrt{2\ln 30-\ln \left( 9x \right)}\ge 0\)?
-
Câu 42:
Trong không gian \(Oxyz\), giao tuyến của 2 mặt phẳng \(\left( \alpha \right):x+2y+z-1=0\) và \(\left( \beta \right):x-y-z+2=0\) có phương trình là?
-
Câu 43:
Cho khối nón đỉnh \(S\) có đáy là đường tròn tâm \(O\), bán kính \(R\). Trên đường tròn \(\left( O \right)\) lấy 2 điểm \(A,B\) sao cho tam giác \(OAB\) vuông. Biết diện tích tam giác \(SAB\) bằng \(\sqrt{2}{{R}^{2}}\). Thể tích khối nón đã cho bằng?
-
Câu 44:
Trong không gian \(Oxyz,\)gọi \(\left( P \right)\) là mp chứa đường thẳng \(d:\frac{x-2}{1}=\frac{y-1}{2}=\frac{z}{-1}\) và cắt trục \(Ox\,,\,Oy\) lần lượt tại \(A\) và \(B\) sao cho đường thẳng \(AB\) vuông góc với \(d\). Phương trình của mặt phẳng \(\left( P \right)\) là?
-
Câu 45:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữa nhật, \(AB=2,\,AD=2\sqrt{3}\), tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc đáy, k/c giữa 2 đường thẳng \(AB\) và \(SC\)bằng \(3\). Tính thể tích của khối chóp \(S.ABCD\) bằng?
-
Câu 46:
Cho hàm số \(f(x)\) có đạo hàm \({f}'(x)=\frac{1}{2}{{x}^{2}}-2x+\frac{3}{2}\) và \(f(0)=0\). Có tất cả bao nhiêu số nguyên \(m\in \left( -2021\,;\,2022 \right)\) để hàm số \(g(x)=\left| {{f}^{2}}(x)+2f(x)+m \right|\) có đúng 3 điểm cực trị?
-
Câu 47:
Có tất cả bao nhiêu cặp số nguyên \(\left( x\,;\,y \right)\) thỏa mãn \({{2.3}^{x-1}}-{{\log }_{3}}\left( {{3}^{x-2}}+2y \right)=6y-x\,+1\) và \({{2022}^{-1}}\le y\le 2022\)?
-
Câu 48:
Trong không gian \(Oxyz\), cho mặt cầu \((S):{{(x+1)}^{2}}+{{(y-1)}^{2}}+{{z}^{2}}=4\) và hai điểm \(A(1\,;\,2\,;\,4)\), \(B(0\,;\,0\,;\,1)\). Mặt phẳng \((P):ax+by+cz+3=0\) \((a,b,c\in \mathbb{R})\) đi qua \(A,B\) và cắt \((S)\) theo giao tuyến là 1 đường tròn có bán kính nhỏ nhất. Giá trị của \(a+b+c\) bằng?
-
Câu 49:
Cho các số phức \(w,\,z\) thỏa mãn \(\left| w+i \right|=\frac{3\sqrt{5}}{5}\) và \(5w=\left( 2+i \right)\left( z-4 \right)\). GTLN của biểu thức \(P=\left| z-1-2i \right|+\left| z-5-2i \right|\) bằng?
-
Câu 50:
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi ĐTHS \(y={{x}^{2}}-4x+4\), trục hoành và trục tung. Đường thẳng \(d\) qua \(A\left( 0\,;\,4 \right)\) và có hệ số góc \(k\,\,\left( k\in \mathbb{R} \right)\) chia hình \(\left( H \right)\) thành 2 phần có diện tích bằng nhau. Giá trị của \(k\) bằng?











