Cho khối nón đỉnh \(S\) có đáy là đường tròn tâm \(O\), bán kính \(R\). Trên đường tròn \(\left( O \right)\) lấy 2 điểm \(A,B\) sao cho tam giác \(OAB\) vuông. Biết diện tích tam giác \(SAB\) bằng \(\sqrt{2}{{R}^{2}}\). Thể tích khối nón đã cho bằng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai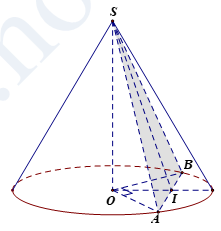
\(\Delta OAB\) vuông tại \(O\)\(\Rightarrow AB=\sqrt{{{R}^{2}}+{{R}^{2}}}=R\sqrt{2}\).
Gọi \(I\) là trung điểm của \(AB\).
Ta có \(\Delta SAB\) cân tại \(S\Rightarrow \)\(SI\) vuông góc với \(AB\).
\({{S}_{\Delta SAB}}=\frac{1}{2}.AB.SI={{R}^{2}}\sqrt{2}\Rightarrow SI=\frac{2.{{R}^{2}}\sqrt{2}}{R\sqrt{2}}=2R\).
Ta lại có \(OI\) là trung tuyến của tam giác vuông \(OAB\)
\(\Rightarrow OI=\frac{AB}{2}=\frac{R\sqrt{2}}{2}\).
\(\Delta SOI\) vuông tại \(O\)\(\Rightarrow SO=\sqrt{S{{I}^{2}}-O{{I}^{2}}}=\sqrt{{{\left( 2R \right)}^{2}}-{{\left( \frac{R\sqrt{2}}{2} \right)}^{2}}}=\frac{\sqrt{14}}{2}R\).
\(V=\frac{1}{3}\pi .O{{A}^{2}}.SO=\frac{1}{3}\pi .{{R}^{2}}.\frac{\sqrt{14}}{2}R=\frac{\sqrt{14}}{6}\pi {{R}^{3}}\).
Chọn A
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Minh Đức