Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình chữ nhật, \(AB=a, AD=a\sqrt2,\,SA\bot(ABCD) \,\mathrm{và}\,SA=a\), (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng (SBD) bằng:

Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai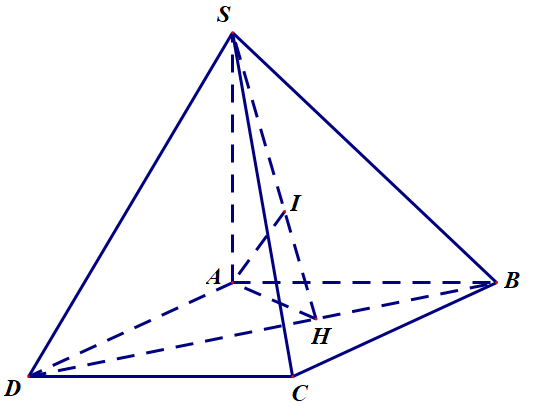
Trong mp (ABCD) kẻ \(AH\bot(ABCD)\)
Kẻ \(AI\bot SH\)
Ta có:\(\left\{ \begin{array}{l} SA \bot BD\\ AH \bot BD \end{array} \right. \Rightarrow DB \bot \left( {SAH} \right) \Rightarrow BD \bot AI\)
Do \(\left\{ \begin{array}{l} AI \bot SH\\ AI \bot BD \end{array} \right. \Rightarrow AI \bot \left( {SBD} \right)\) nên AI là khoảng cahcs từ A đến (SBD)
Tam giác ABD vuông tại A và có đường cao AH nên
\(\begin{array}{l} \frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{2{a^2}}} = \frac{3}{{{2a^2}}}\\ \end{array}\)
Tam giác SAH vuông tại A có đường cao AI nên
\(\begin{array}{l} \frac{1}{{A{I^2}}} = \frac{1}{{A{H^2}}} + \frac{1}{{SA^2}} = \frac{3}{{{2a^2}}} + \frac{1}{{{a^2}}} = \frac{5}{{{2a^2}}}\\ \Rightarrow A{I^2} = \frac{{{2a^2}}}{5} \Rightarrow AI= \frac{a\sqrt{10}}{5} \end{array}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Khoa Học Tự Nhiên lần 3
















