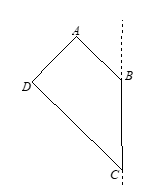
Cho hình thang ABCD vuông tại A và D có \(CD=2AB=2AD=6.\) Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quanh xung quanh đường thẳng BC

 

Câu hỏi liên quan

• Cho hàm số \(y={{x}^{3}}-6{{x}^{2}}+9x+m\text{ }\left( C \right)\), với \(m\) là tham số. Giả sử đồ thị \(\left( C \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}\). Khẳng định nào sau đây đúng?

• Cho hàm số \(y=\frac{x+2}{x-1}\). Xét các mệnh đề sau:

  1) Hàm số đã cho đồng biến trên \(\left( 1;+\infty  \right).\)

  2) Hàm số đã cho nghịch biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}.\)

  3) Hàm số đã cho không có điểm cực trị.

  4) Hàm số đã cho nghịch biến trên các khoảng \(\left( -\infty ;1 \right)\) và \(\left( 1;+\infty  \right).\)

  Số các mệnh đề đúng là

• Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(AC=2a\). Hình chiếu vuông góc của \({A}'\) trên mặt phẳng \(\left( ABC \right)\) là trung điểm \(H\) của cạnh \(AB\) và \(A{A}'=a\sqrt{2}\). Tính thể tích \(V\) của khối lăng trụ đã cho.

ZUNIA12

• Cho hình chóp \(S.ABC\) có \(AB=4a,BC=3\sqrt{2}a,\)\(\widehat{ABC}=45{}^\circ ;\widehat{SAC}=\widehat{SBC}=90{}^\circ \); Sin góc giữa hai mặt phẳng\(\left( SAB \right)\)và\(\left( SBC \right)\) bằng\(\frac{\sqrt{2}}{4}.\) Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng

• Cho có tháp nước như hình dưới đây, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m, chiều cao hình trụ là 2m, chiều cao của hình nón là 1m.

  Thể tích của toán bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?

  

• Gọi \(l,h,r\) lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy. Diện tích xung quanh

  \({{S}_{xq}}\) của hình nón là: 

• Nghiệm của phương trình \({{\left( \frac{1}{5} \right)}^{{{x}^{2}}-2x-3}}={{5}^{x+1}}\) là 

• Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y=\ln \left( {{x}^{2}}-2mx+4 \right)\) có tập xác định là \(\mathbb{R}.\) 

• Cho hàm số \(y=f\left( x \right)\) xác định trên tập \(D\). Số \(M\) được gọi là giá trị lớn nhất của hàm số \(y=f\left( x \right)\) trên \(D\) nếu

• Cho đồ thị hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

  

  Số nghiệm của phương trình \(\left| 2f\left( x \right)-3 \right|=1\) là

• Mệnh đề nào dưới đây sai? 

• Một hộp có 6 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ ba màu và số viên bi đỏ lớn hơn số viên bi vàng.

• Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y={f}'\left( x \right)\)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.

  

  Hàm số \(y=f\left( x \right)\)nghịch biến trên 

• Cho phương trình \(\left( 4\log _{2}^{2}x+{{\log }_{2}}x-5 \right)\sqrt{{{7}^{x}}-m}=0\) (\(m\) là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của  để phương trình đã cho có đúng hai nghiệm phân biệt?

• Cho biểu thức \(\sqrt[3]{4\sqrt{2\sqrt[5]{8}}}={{2}^{\frac{m}{n}}}\), trong đó \(\frac{m}{n}\) là phân số tối giản. Gọi \(P={{m}^{2}}+{{n}^{2}}\). Khẳng định nào sau đây đúng? 

• Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) có bảng xét dấu của \({f}'\left( x \right)\) như sau:

  

  Số điểm cực tiểu của hàm số đã cho là

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=3,\,AD=4\) và các cạnh bên của hình chóp tạo với mặt đáy một góc \(60{}^\circ \). Tính thể tích khối cầu ngoại tiếp hình chóp đã cho. 

• Cho hình trụ có hai đáy là hai hình tròn \(\left( O \right)\) và \(\left( O' \right)\), thiết diện qua trục của hình trụ là hình vuông. Gọi\(A\) và \(B\)là hai điểm lần lượt nằm trên hai đường tròn\(\left( O' \right)\)và \(\left( O \right)\). Biết \(AB=2a\) và khoảng cách giữa \(AB\) và \(OO'\)bằng\(\frac{a\sqrt{3}}{2}\). Tính diện tích xung quanh của hình trụ.

• Tập nghiệm của bất phương trình \({{2}^{x\,-\,3}}\,>\,8\) là

• Gọi \(n\) là số nguyên dương bất kì, \(n\ge 2\), công thức nào dưới đây đúng?