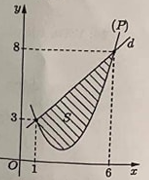
Cho khối chóp S.ABCD có đáy ABCD là hình bình hành, SA = SB = SC = AC = a,SB tạo
với mặt phẳng (SAC) một góc 30°. Thể tích của khối chóp đã cho bằng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn C
Vẽ \(BH \bot \left( {SAC} \right)\) tại H suy ra \(\left( {SB;\left( {SAC} \right)} \right) = \left( {SB;BH} \right) = \widehat {BSH} = 30^\circ \).
Từ đó ta có \({V_{S.ABCD}} = 2{V_{S.ABC}} = 2{V_{B.SAC}}\).
Xét \(\Delta SHB\) vuông tại H ta có \(\sin \widehat {BSH} = \frac{{BH}}{{SB}} \Rightarrow \sin 30^\circ = \frac{{BH}}{a} \Leftrightarrow BH = \frac{a}{2}\)
Ta có \({V_{B.SAC}} = \frac{1}{3}BH.{S_{\Delta SAC}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{24}}\).
Vậy \({V_{S.ABCD}} = 2{V_{B.SAC}} = 2.\frac{{{a^3}\sqrt 3 }}{{24}} = \frac{{{a^3}\sqrt 3 }}{{12}}\).
Đề thi tốt nghiệp THPT môn Toán năm 2023
Bộ GD&ĐT - Mã đề 101