Có bao nhiêu giá trị nguyên của tham số m sao cho ứng với mỗi m, hàm số \(y=\text{ }-{{x}^{3}}+3{{x}^{2}}-3mx+\frac{5}{3}\) có đúng một điểm cực trị thuộc khoảng (-2;5)?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
Ta có: \(y' = - 3{x^2} + 6x - 3m\).
Hàm số \(y = - {x^3} + 3{x^2} - 3mx + \frac{5}{3}\) có đúng 1 cực trị thuộc khoảng (-2; 5).
Khi và chỉ khi y' = 0 có 1 nghiệm thuộc khoảng (-2; 5).
\(\Leftrightarrow {x^2} - 2x + m = 0\) có 1 nghiệm thuộc khoảng (-2; 5).
\( \Leftrightarrow {x^2} - 2x = - m\).
Cho \(g\left( x \right) = {x^2} - 2x \Rightarrow g'\left( x \right) = 2x - 2\).
\(g'\left( x \right) = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\).
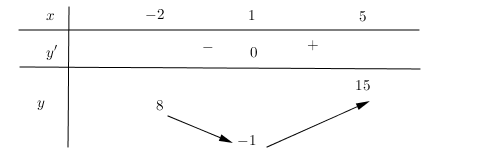
Để hàm số có 1 cực trị :
\(\begin{array}{l}
\Rightarrow 8 \le - m < 15 \Leftrightarrow - 15 < m \le - 8\\
\Rightarrow m \in \left\{ { - 14; - 13; - 12; - 11; - 10; - 9; - 8} \right\}
\end{array}\).
Đề thi tốt nghiệp THPT môn Toán năm 2023
Bộ GD&ĐT - Mã đề 101