Cho lăng trụ tam giác đều \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có độ dài cạnh đáy bằng a, góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng \(60^{\circ} .\) . Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai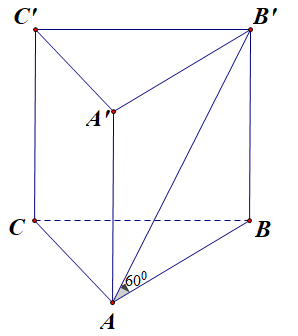
Ta có: \(\widehat {\left(A B^{\prime} ;(A B C)\right)}=\widehat{Ơ\left(A B^{\prime} ; A B\right)}=\widehat{B A B^{\prime}}=60^{\circ}\)
\(\tan\widehat{ B A B^{\prime}}=\frac{B B^{\prime}}{A B} \Rightarrow B B^{\prime}=A B \cdot \tan \widehat{B A B^{\prime}}=a \cdot \tan 60^{\circ}=a \sqrt{3}\)
Bán kính đường tròn ngoại tiếp đáy lăng trụ:\(R=\frac{a \sqrt{3}}{3}\)
\(\Rightarrow V=S \cdot h=\pi\left(\frac{a \sqrt{3}}{3}\right)^{2} \cdot a \sqrt{3}=\frac{\pi a^{3} \sqrt{3}}{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Nguyễn Trãi