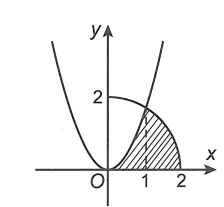
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol \(y=\sqrt{3}{{x}^{2}}\), cung tròn có phương trình \(y=\sqrt{4-{{x}^{2}}}\) (với \(0\le x\le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) là

Câu hỏi liên quan

• Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\text{ }\!\![\!\!\text{ }-1;\,2]\) và \(f\left( -1 \right)=2023,\,f\left( 2 \right)=-1. \)Tích phân \(\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}\)bằng:

• Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=16\) và điểm \(A\left( -1;-1;-1 \right).\) Xét các điểm M thuộc \(\left( S \right)\)sao cho đường thẳng AM tiếp xúc với \(\left( S \right).\) M luôn thuộc một mặt phẳng cố định có phương trình là

• Cho số phức \(z\)thỏa mãn \(\left( 1+i \right)z=14-2i\). Tổng phần thực và phần ảo của \(\overline{z}\) bằng

ZUNIA12

• Gọi \({{z}_{1}}\) là nghiệm phức có phần ảo âm của phương trình \({{z}^{2}}-2z+5=0\). Tọa độ điểm biểu diễn số phức \(\frac{7-4i}{{{z}_{1}}}\) trên mặt phẳng phức là

• Cho tam giác \(ABC\)có trọng tâm \(G\). Mệnh đề nào sau đây là mệnh đề SAI?

• Đặt \(a={{\log }_{2}}5,\,b={{\log }_{3}}5\). Hãy biểu diễn \({{\log }_{6}}5\)theo \(a\) và \(b\).

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA=a\) và \(SA\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABCD\) bằng

• Cho số phức \(z=-1-2\sqrt{6}i\). Phần thực và phần ảo của số phức \(\overline{z}\) là?

• Cho điểm \(M\left( 1,-4,-2 \right)\) và mặt phẳng \(\left( P \right):x+y+5z-14=0\). Tính khoảng cách từ \(M\) đến \((P)\).

• Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng \(A{B}'\) và \(C{C}'\) bằng

  

• Hàm số nào dưới đây có bảng biến thiên như sau:

   

• Phương trình tiếp tuyến của đường cong \(y={{x}^{3}}+3{{x}^{2}}-2\) tại điểm có hoành độ \({{x}_{0}}=1\) là

• Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy hai điểm \(A,B\) phân biệt thuộc \(a\) và hai điểm \(C,D\) phân biệt thuộc \(b\). Khi đó hai đường thẳng \(A\text{D}\) và \(BC\) ở vị trí

• Tập nghiệm của bất phương trình \({{3}^{{{x}^{2}}-13}}<27\) là

• Cho hai tích phân \(\int\limits_{-2}^{5}{f\left( x \right)\text{d}}x=8\) và \(\int\limits_{5}^{-2}{g\left( x \right)\text{d}}x=3\). Tính \(I=\int\limits_{-2}^{5}{\left[ f\left( x \right)-4g\left( x \right)-1 \right]\text{d}}x\)

• Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng \(a\) có diện tích bằng \(8{{a}^{2}}\sqrt{3}\). Thể tích của khối trụ là

• Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông cân tại \(C\) và \(SA\) vuông góc với mặt phẳng đáy. Cho \(SC=a\), mặt phẳng \(\left( SBC \right)\) tạo với mặt đáy một góc \(\alpha \). Thể tích khối chóp \(S.ABC\) đạt giá trị lớn nhất là

• Trong không gian \(\text{Ox}yz\), đường thẳng \(d:\,\frac{x-1}{1}=\frac{y-3}{3}=\frac{z+4}{-2}\) đi qua điểm nào dưới đây?

• Đạo hàm của hàm số \(y={{8}^{x}}\) là

• Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ -1;1 \right\}\), thỏa mãn \(f'\left( x \right)=\frac{2}{{{x}^{2}}-1};\ f\left( -3 \right)+f\left( 3 \right)=2\ln 2\) và \(f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=0\). Giá trị của biểu thức \(P=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)\) là: