Có bao nhiêu giá trị nguyên của m để phương trình \(log_2{mx}=log_{\sqrt2}(x+1)\) vô nghiệm
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐKXĐ: \(\left\{ \begin{array}{l} mx > 0\\ x + 1 > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} mx > 0\\ x > - 1 \end{array} \right.\)
Ta có:
\(\begin{array}{l} {\log _2}mx = {\log _{\sqrt 2 }}\left( {x + 1} \right)\,\,\,\,(1)\\ \Leftrightarrow {\log _2}mx = 2{\log _2}\left( {x + 1} \right)\\ \Leftrightarrow {\log _2}mx = {\log _2}{\left( {x + 1} \right)^2}\\ \Leftrightarrow mx = {\left( {x + 1} \right)^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \end{array}\)
Phương trình (1) có nghiệm khi và chỉ khi phương trình (2) có nghiệm thỏa x+1>0
Xét phương trình (2)
- Nếu x=0 thì mx=0, không thỏa điều kiện nên loại nghiệm x=0.
- Nếu \(x\ne 0\) thì (2) \(\Leftrightarrow m = \frac{{{{\left( {x + 1} \right)}^2}}}{x}\)
Xét hàm số \(f(x) = \frac{{{{\left( {x + 1} \right)}^2}}}{x}\) trên tập xác định \(D = \left( { - 1; + \infty } \right)\backslash {\rm{\{ }}0\} \)
\(f'(x)=\frac{x^2-1}{x^2}\), f'(x) không xác định tại x=0
\(f'(x)=0\Leftrightarrow\frac{x^2-1}{x^2}=0 \Leftrightarrow x = \pm 1\)
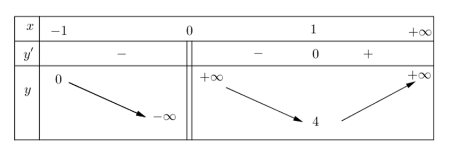
Từ bảng biến thiên suy ra để phương trình vô nghiệm thì \(0 \le m < 4\).
Vậy \(m \in {\rm{\{ 1;2;3;4\} }}\) thì phương trình vô nghiệm.
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Khoa Học Tự Nhiên lần 3
Câu hỏi liên quan
-
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=3, AD=4, AA'=5. Gọi O là tâm của đáy ABCD. Thê tích khối chóp O.A'B'C' bằng
-
Cho cấp số cộng \((u_n)\) có công sai d=2, \(u_1=-1\). Giá trị của \(u_5\) bằng
-
Hàm số nào dưới đây có đồ thị như trong hình bên
-
Cho đồ thị hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị f'(x) như hình vẽ. Số điểm cực đại của hàm số \(g(x)=f(-x^2+x)\) là
-
Tập xác định của hàm số \(y = {\log _3}(x - 2)\) là
-
Cho hàm số y = f (x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f (1- f (x)) = 2\) là:
-
Xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang. Xác suất để 2 bạn nữ không ngồi cạnh nhau
bằng -
Cho hàm số f(x) có bảng biến thiên
Số nghiệm của phương trình 2f(x)-3=0 là
-
Trong không gian Oxyz, cho mặt phẳng (P): \(-x+3y-2z+1=0\). Vectơ nào sao đây là một vec tơ pháp tuyến của (P)
-
Cho hàm số \(y={\sqrt{x-2}\over(x^2-4)(2x-7)}\). Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
-
Cho hàm số \(y=f(x)\) biết \(f(0)=\frac{1}{2}\) và \(f'(x)=xe^{x^2}\) với mọi \(x\in\mathbb{R}\). Khi đó \(\int\limits_0^1 {xf(x)dx} \) bằng
-
Cho hàm số y=f(x) xác định trên \(\mathbb{R}\), có đồ thị f(x) như hình vẽ. Hàm số \(g(x)=f(x^3+x)\) đạt cực tiểu tại điểm x0. Giá trị x0 thuộc khoảng nào dưới đây
-
Tập hợp tất cả các giá trị của tham số m để hàm số \(v=\frac{mx-4}{x-m}\) đồng biến trên khoảng \((-1;+\infty)\) là
-
Đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 3}}\) có tất cả bao nhiêu đường tiệm cận
-
Nghiệm của phương trình \(3^{x+2}=27\) là
-
Trong không gian Oxyz, cho các điểm A(1;-1;2) và đường thẳng \(d:\,\left\{ \begin{array}{l} x = 1 + t\\ y = 1 - t\\ z = 1 + 2t \end{array} \right.\). Phương trình mặt phẳng qua A và vuông góc với d là
-
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại C, AB=2a và góc tạo bởi hai mặt phẳng (ABC') và (ABC) bằng 600. Gọi M , N lần lượt là trung điểm của A'C' và BC . Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng:
-
Đạo hàm của hàm số \(y=log_{2002}{(x^2+x)}\) là
-
Cho x,y là các số thực dương thỏa mãn \({\log _2}\frac{{3x + 3y + 4}}{{{x^2} + {y^2}}} = \left( {x + y - 1} \right)\left( {2x + 2y - 1} \right) - 4\left( {xy + 1} \right)\). Giá trị lớn nhất của biểu thức \(P = \frac{{5x + 3y - 2}}{{2x + y + 1}}\) bằng:
-
Trong hệ tọa độ Oxyz cho hai điểm A(-1;2;1), B(1;2;-3). Mặt cầu đường kính AB có phương trình
