Trên một cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa 2 cọc là 4 mét còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung.
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.jpg.png)
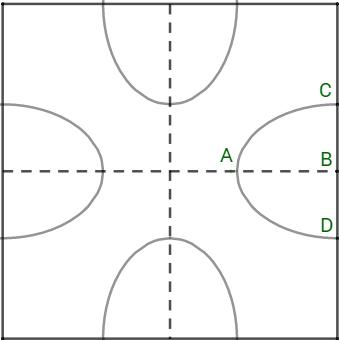
Gọi \(\left( {{C_1}} \right):{x^2} + {y^2} = 9 \vee \left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {y^2} = 4\) là phương trình hai đường tròn biểu diễn phần ăn cỏ của 2 con bò.
Xét phần phía trên Ox
\(\begin{array}{l} \left( {{C_1}} \right):{x^2} + {y^2} = 9 \Rightarrow y = \sqrt {9 - {x^2}} \\ \left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {y^2} = 4 \Rightarrow y = \sqrt { - {x^2} + 8x - 12} \end{array}\)
Phương trình hoành độ giao điểm \(\sqrt {9 - {x^2}} = \sqrt { - {x^2} + 8x - 12} \Leftrightarrow x = \frac{{21}}{8}\)
Vậy \(S = 2\left[ {\int\limits_2^{\frac{{21}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{21}}{8}}^3 {\sqrt {9 - {x^2}} } {\rm{d}}x} \right]\)
\(I = \int\limits_{\frac{{21}}{8}}^3 {\sqrt {9 - {x^2}} } {\rm{d}}x\mathop = \limits^{x = 3\sin t} \int\limits_{\arcsin \frac{7}{8}}^{\frac{\pi }{6}} {9{{\cos }^2}t{\rm{d}}t} = 9.\int\limits_{\arcsin \frac{7}{8}}^{\frac{\pi }{6}} {\frac{{\cos 2t + 1}}{2}{\rm{d}}t = \left. {9\left( {\frac{1}{4}\sin 2t + \frac{t}{2}} \right)} \right|} _{\arcsin \frac{7}{8}}^{\frac{\pi }{6}} \approx 0,3679\)
\(J = \int\limits_2^{\frac{{21}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x\mathop = \limits^{x - 4 = 2\sin t} \int\limits_{ - \frac{\pi }{2}}^{\arcsin \left( { - \frac{{11}}{{16}}} \right)} {4{{\cos }^2}t{\rm{d}}t} = 4.\int\limits_{ - \frac{\pi }{2}}^{\arcsin \left( { - \frac{{11}}{{16}}} \right)} {\frac{{\cos 2t + 1}}{2}{\rm{d}}t = \left. {4\left( {\frac{1}{4}\sin 2t + \frac{t}{2}} \right)} \right|} _{ - \frac{\pi }{2}}^{\arcsin \left( { - \frac{{11}}{{16}}} \right)} \approx 0,627\)
\(\Rightarrow S \approx 1,9898\)
Đề thi thử THPT QG năm 2021 môn Toán
Trường THPT Nguyễn Văn Thoại lần 2
.jpg.png)
.jpg.png)
.jpg.png)











