Trong không gian Oxyz, xét mặt cầu (S) có tâm I(4;8; 12) và bán kính R thay đổi. Có bao nhiêu giá trị nguyên của R sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của (S) trong mặt phẳng (Oyz) mà hai tiếp tuyến đó cùng đi qua 0 và góc giữa chúng không nhỏ hơn 600?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
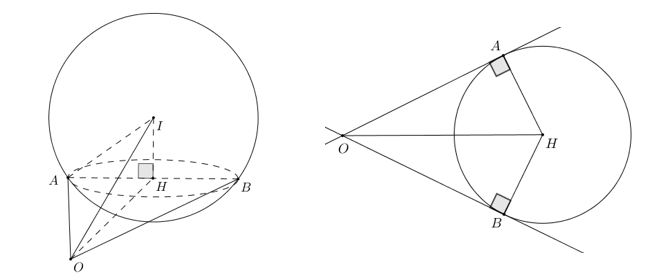
Giả sử 2 tiếp tuyến OA, OB, theo giả thiết ta có \(\left( {\overrightarrow {OA} ,\,\overrightarrow {OB} } \right) \ge 60^\circ \).
Suy ra \(30^\circ \le \widehat {AOH} \le 60^\circ \).
Gọi H là hình chiếu của I trên (Oyz) \( \Rightarrow H\left( {0;\,8;\,12} \right) \Rightarrow OH = 4\sqrt {13} \).
Xét tam giác OAH có: \(HA = OH\sin \widehat {AOH} \ge 4\sqrt {13} \sin 30^\circ = 2\sqrt {13} \).
Ta có \(2\sqrt {13} \le HA < 2\sqrt {39} \) \( \Rightarrow 52 \le A{H^2} \le 156\)
\( \Rightarrow 52 + 16 \le A{H^2} + I{H^2} \le 156 + 16\)
\( \Rightarrow 68 \le I{A^2} \le 172 \Rightarrow 68 \le {R^2} \le 172$ hay $8,24 \le R \le 13,11\).
\( \Rightarrow R \in \left\{ {9;\,10;\,...;\,13} \right\}\).
Vậy có tất cả 5 giá trị của R.
Đề thi tốt nghiệp THPT môn Toán năm 2023
Bộ GD&ĐT - Mã đề 101