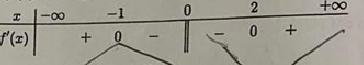Cho hàm số f(x) = x4 – 32x2 + 4. Có bao nhiều giá trị nguyên của tham số m sao cho ứng với mỗi m, tổng giá trị các nghiệm phân biệt thuộc khoảng (-3;2) của phương trình f(x2 + 2x + 3) = m bằng – 4?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
- Phương trình \({x^2} + 2x + 3 = a\,\,\left( {a \in ℝ } \right)\) có hai nghiệm \({x_1},{x_2}\)
Thì ta có: \({x_1} + {x_2} = - 2\).
- Phương trình \(f\left( {{x^2} + 2{\rm{x}} + 3} \right) = m\left( 1 \right)\) có tổng nghiệm bằng -4.
Tương đương pt (1) có nghiệm xảy ra ở trường hợp: 4 nghiệm phân biệt \({x_1},{x_2},{x_3},{x_4}\,\,\left( 2 \right)\)
( do khi đó: \(\left( {{x_1} + {x_2}} \right) + \left( {{x_3} + {x_4}} \right) = - 2 + \left( { - 2} \right) = - 4\,\,\))
Đặt \({x^2} + 2x + 3 = t\).
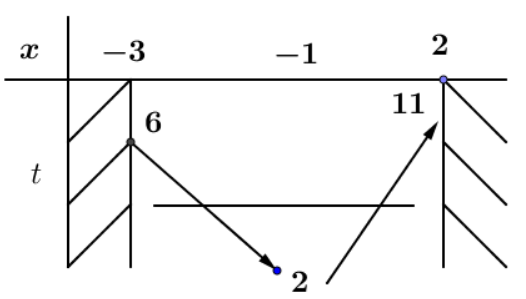
Điều kiện (2) ↔ Tìm m để phương trình \(f\left( t \right) = m\) có 2 nghiệm \(2 < t < 6\,\,\,(2)\).
Xét \(f\left( t \right) = {t^4} - 32{t^2} + 4\)
\( \Rightarrow f'\left( t \right) = 4{t^3} - 64t \Rightarrow f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
t = 0\\
t = \pm 4
\end{array} \right.\)

Yêu cầu bài toán số \( \Leftrightarrow - 252 < m < - 108\) \( \Rightarrow \,143\) số.
Đề thi tốt nghiệp THPT môn Toán năm 2023
Bộ GD&ĐT - Mã đề 101