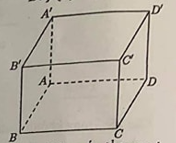
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, BC = 2, AA' = 2 (tham khảo hình bên). Khoảng cách giữa hai đường thẳng AD và DC' bằng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
Ta có \(AD' \subset \left( {AD'B'} \right),DC' \subset \left( {DC'B} \right)\) và \(\left( {AD'B'} \right){\rm{ // }}\left( {DC'B} \right)\)
Nên khoảng cách giữa hai đường thẳng AD' và DC' bằng khoảng cách giữa \(\left( {AD'B'} \right)\) và \(\left( {DC'B} \right)\).
\(d\left( {\left( {AD'B'} \right);\left( {DC'B} \right)} \right) = d\left( {A;\left( {DC'B} \right)} \right) = d\left( {C;\left( {DC'B} \right)} \right) = h\).
Xét tứ diện \(C.BC'D\) có các cạnh \(CD,CB,CC'\) đôi một vuông góc nên ta có:
\(\begin{array}{l}
\frac{1}{{{h^2}}} = \frac{1}{{C{B^2}}} + \frac{1}{{C{D^2}}} + \frac{1}{{CC{'^2}}} = \frac{1}{{{2^2}}} + \frac{1}{{{1^2}}} + \frac{1}{{{2^2}}} = \frac{3}{2}\\
\Rightarrow h = \frac{{\sqrt 6 }}{3}
\end{array}\)
Đề thi tốt nghiệp THPT môn Toán năm 2023
Bộ GD&ĐT - Mã đề 101