Xét khối nón (N) có đỉnh và đường tròn đáy cùng nằm trên một mặt cầu bán kính bằng 2. Khi (N) có độ dài đường sinh bằng 2V3, thể tích của nó bằng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn B
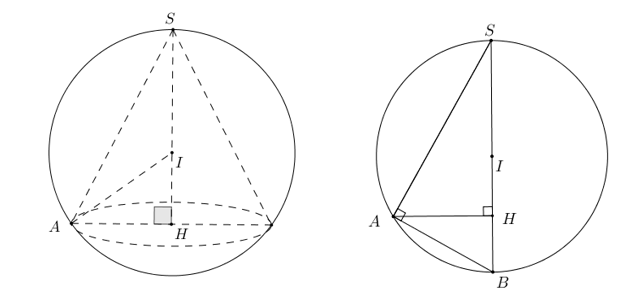
Gọi H là tâm đường tròn đáy của (N), đỉnh S.
TH1: I thuộc đoạn SH. Đặt \(IH = x,\,\,\left( {0 < x < 2} \right)\), suy ra \(AH = \sqrt {I{A^2} - I{H^2}} = \sqrt {4 - {x^2}} \)
Ta có \(S{A^2} = S{H^2} + H{A^2}\)
Suy ra \(12 = {\left( {2 + x} \right)^2} + 4 - {x^2} \Leftrightarrow x = 1\,\left( {t.m} \right)\)
Suy ra \(SH = 3,AH = \sqrt 3 \Rightarrow V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .3.3 = 3\pi \)
TH2: H thuộc đoạn SI. Đặt \(IH = x,\,\,\left( {0 < x < 2} \right)\), suy ra \(AH = \sqrt {I{A^2} - I{H^2}} = \sqrt {4 - {x^2}} \)
Ta có \(S{A^2} = S{H^2} + H{A^2}\)
Suy ra \({\left( {2\sqrt 3 } \right)^2} = {\left( {2 - x} \right)^2} + 4 - {x^2} \Leftrightarrow x = - 1\,\) (loại)
Đề thi tốt nghiệp THPT môn Toán năm 2023
Bộ GD&ĐT - Mã đề 101