Cho A(2;1) . Tìm điểm B trên trục hoành và điểm C trên đường phân giác góc phần tư thứ nhất để chu vi tam giác ABC nhỏ nhất
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai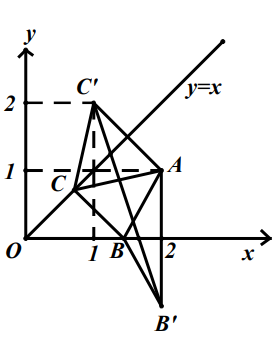
Gọi B',C' lần lượt là ảnh của A qua các phép đối xứng trục có trục là Ox,Oy , khi đó ta có \(B^{\prime}(2 ;-1), C^{\prime}(1 ; 2)\)
Ta có \(A B=B B^{\prime}, A C=A C^{\prime}\) nên chu vi tam giác ABC là:
\(\begin{array}{l} 2 p=A B+B C+C A \\ =A B^{\prime}+B C+C C^{\prime} \geq B^{\prime} C^{\prime}=\sqrt{10} \end{array}\)
Đẳng thức xảy ra khi B và C là các giao điểm của B'C' với Ox và đường phân giác góc phần tư thứ nhất, từ đó không khó khăn gì ta tìm được \(B^{\prime}\left(\frac{5}{3} ; 0\right) \text { và } C^{\prime}\left(\frac{5}{4} ; \frac{5}{4}\right)\)
Câu hỏi liên quan
-
Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
-
Trong mặt phẳng Oxy, thực hiện liên tiếp ghép đối xứng trục Oy và ghép quay tâm O góc quay 90o biến điểm M(1;1) thành điểm M’’. tọa độ M’’ là:
-
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
-
Tam giác đều có bao nhiêu trục đối xứng?
-
Trong các mệnh đề sau mệnh đề nào đúng?
-
Trong mặt phẳng tọa độ Oxy cho đường tròn \((C):(x-1)^{2}+(y+2)^{2}=4\) . Phép đối xứng trục Ox biến đường tròn (C) thành đường tròn (C ') có phương trình là:
-
Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình H . Hỏi H có mấy trục đối xứng?
-
Hình nào có số trục đối xứng nhỏ nhất
.png)
-
Trong các mệnh đề sau mệnh đề nào đúng?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình
-
Trong mặt phẳng tọa độ Oxy qua phép đối xứng trục Oy , điểm A(3;5) biến thành điểm nào trong các điểm sau?
-
Đồ thị của hàm số \(y=\cos x\)có bao nhiêu trục đối xứng?
-
Trong mặt phẳng Oxy , cho đường thẳng \(d: x+2 y+4=0\) . Tìm ảnh của d qua phép đối xứng trục Ox
-
Trong mặt phẳng Oxy cho điểm M(2;3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
-
Trong mặt phẳng tọa độ Oxy cho parabol \((P): y=x^{2}-2 x+3\) Phép đối xứng trục Ox biến parabol (P) thành parabol (P ′) có phương trình là:
-
Trong mặt phẳng Oxy , cho điểm M(2 ; 3) . Hỏi trong bốn điểm sau điểm nào là ảnh của M qua phép đối xứng qua đường thẳng d: x-y=0 ?
-
Hình nào sau đây không có trục đối xứng (mỗi hình là một chữ cái in hoa):
-
Trong mặt phẳng tọa độ Oxy, cho biết A(3,5) Tìm tọa độ A’ là ảnh của điểm A qua phép đối xứng trục Ox.
-
Trong mặt phẳng tọa độ Oxy cho đường thẳng \(d: x+y-2=0\) Ảnh của đường thẳng d qua phép đối xứng trục Ox có phương trình là:
