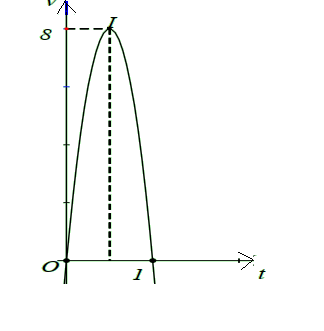
Cho đồ thị biểu thị vận tốc của hai xe A và B khởi hành cùng một lúc, bên cạnh nhau và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường Parabol, đồ thị biểu diễn vận tốc của xe B là một đường thẳng ở hình bên. Hỏi sau khi đi được 3 giây, khoảng cách giữa hai xe là bao nhiêu mét?

Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{{x \over 2}}},y = 0,x = 0\) và \(x = 1\).
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Một nhóm sinh viên được thực hành nghiên cứu sự chuyển động của các hạt. Nhóm đã phát hiện hạt prô-ton di chuyển trong điện trường với gia rốc \(a=-\frac{20}{(1+2 t)^{2}}\left(\mathrm{~cm} / \mathrm{s}^{2}\right)\) . Nhóm sinh viên đã tìm ra hàm vận tốc của hạt đó, biết khi t = 0 thì vận tốc là \(v=30 \mathrm{~cm} / \mathrm{s}\) . Biểu thức đúng là? 

Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y = - {x^2}\), trục hoành, và hai đường thẳng \(x = - 1;x = 2\).

Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường \(y=\sqrt{x}\) và y=x quanh trục Ox bằng

 Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x³ - x và đồ thị hàm số y = x - x².

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\), trục Ox và hai đường thẳng \(x=1, x=2\). Khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục Ox có thể tích là

Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi \(\displaystyle  {x^2} + {y^2} = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle  Ox\) là một hình vuông.

Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = 2 - x,y = {x^2}\) và trục hoành trong miền \(x \ge 0\)

Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng xác định bởi \(\displaystyle  y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(\displaystyle  y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ \(\displaystyle  x = 1\), quanh trục \(\displaystyle  Oy\)

Diện tích của hình phẳng giới hạn bởi các đường \(y = x^2+ 1 , y = 0, x = - 1, x = 2 \) bằng:

Một vật chuyển động trong 3 giờ với vận tốc v(km/h)  phụ thuộc thời gian t(h) có đồ thị của vận tốc là một phần của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó

Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a, x=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?

Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích (S₁,S₃ ) dùng để trồng hoa, phần diện tích  (S₂,S₄ ) dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là (150.000 ) đồng/ (m² ), kinh phí trồng cỏ là (100.000 ) đồng/ (m² ). Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).

Cho nửa đường tròn đường kính (\(AB=4\sqrt5\) ). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần gạch chéo trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:

Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = -1\) và \(x = 1\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x( - 1 \le x \le 1)\) là một hình vuông cạnh là \(2\sqrt {1 - {x^2}} \).

Cho hàm số \(y=f( x ) ,y=g( x )\) liên tục trên [ a;b ]. Gọi  H là hình phẳng giới hạn bởi hai đồ thị y=f( x ), y=g( x) và các đường thẳng x=a, x=b. Diện tích H được tính theo công thức 

Nam và Hùng tập sút phạt, ai sút trúng gôn nhiều hơn là người thẳng cuộc. Nếu để bóng ở vị trí A thì xác suất trúng vào gôn của Nam là 0,9 còn của Hùng là 0,7. Nếu để bóng ở vị trí B thì xác suất trúng vào gôn của Nam là 0,7 còn của Hùng là 0,8. Nam và Hùng đều đá một quả ở vị trí A và một quả ở vị trí B. Xác suất để Nam thắng cuộc là:

Tính thể tích khối tròn xoay khi quay hình phẳng xác định bởi: \(\displaystyle  y = {(2x + 1)^{\frac{1}{3}}},x = 0,y = 3\), quanh trục \(\displaystyle  Oy\).

Quay hình phẳng (H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay
có thể tích là

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sin x, trục hoành, trục tung và đường  thẳng \(x = 2\pi \)