Cho hàm số\(y=x^{4}-3 x^{2}+m\) có đồ thị (Cm ) , với m là tham số thực. Giả sử (Cm ) cắt trục Ox tại bốn điểm phân biệt như hình vẽ
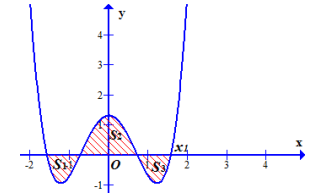
Gọi \(S_{1}, S_{2}, S_{3}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để \(S_{1}+S_{3}=S_{2}\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi \(x_1\) là nghiệm dương lớn nhất của phương trình
\(x^{4}-3 x^{2}+m=0, \text { ta có } m=-x_{1}^{4}+3 x_{1}^{2}\,\,\,\,(1)\)
Vì \(S_{1}+S_{3}=S_{2} \text { và } S_{1}=S_{3} \text { nên } S_{2}=2 S_{3} \text { hay } \int_{0}^{x_{1}} f(x) \mathrm{d} x=0\)
Mà \(\int_{0}^{x_{1}} f(x) \mathrm{d} x=\int_{0}^{x_{1}}\left(x^{4}-3 x^{2}+m\right) \mathrm{d} x=\left.\left(\frac{x^{5}}{5}-x^{3}+m x\right)\right|_{0} ^{x_{1}}=\frac{x_{1}^{5}}{5}-x_{1}^{3}+m x_{1}=x_{1}\left(\frac{x_{1}^{4}}{5}-x_{1}^{2}+m\right)\)
Do đó: \(x_{1}\left(\frac{x_{1}^{4}}{5}-x_{1}^{2}+m\right)=0 \Leftrightarrow \frac{x_{1}^{4}}{5}-x_{1}^{2}+m=0\,\,\,\,\,\,(2) \left(\text { vì } x_{1}>0\right)\)
Từ (1) và (2) ta có:
\(\frac{x_{1}^{4}}{5}-x_{1}^{2}-x_{1}^{4}+3 x_{1}^{2}=0 \Leftrightarrow-4 x_{1}^{4}+10 x_{1}^{2}=0 \Leftrightarrow x_{1}^{2}=\frac{5}{2}\)
Vậy \(m=-x_{1}^{4}+3 x_{1}^{2}=\frac{5}{4}\)