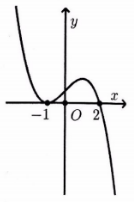
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị trên đoạn \(\left[ {0;4} \right]\) như hình vẽ bên dưới

Đặt \(M = \max f\left( {\sqrt {4 – {x^2}} } \right),m = \min f\left( {\sqrt {4 – {x^2}} } \right)\). Tổng M + m bằng

Câu hỏi liên quan

• Tìm giá trị nhỏ nhất của hàm số \(y=f(x)=\sqrt{x-2}+\sqrt{8-x}\)

• Hàm số y = x⁸ + (x⁴ – 1) ² + 5  đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2]  lần lượt tại hai điểm có hoành độ x₁; x₂. Khi đó tích x₁.x₂ có giá trị bằng:

• Trong các hình trụ nội tiếp hình cầu bán kính R, hình trụ có thể tích lớn nhất bằng

ZUNIA12

• \(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x - 9}}{{x + 3}}\text{ trên đoạn } \left[ { - 5; - 4} \right]\)

• Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f(x) trên [ a; e]?

  

• Tìm m để bất phương trình x²-5mx+9 ≥ 0 có nghiệm x ?

• Giá trị nhỏ nhất của hàm số \(y=x(x+2)(x+4)(x+6)+5\) trên nữa khoảng \([-4 ;+\infty)\)

• Tìm GTLN của hàm số \(y = x - \sqrt {{x^2} + 1} \) ?

• Hàm số y = x³ – 2x² – 7x + 5 có giá trị nhỏ nhất là m và giá trị lớn nhất là M trên đoạn [1;3]. Khi đó tổng m + M bằng

• Gọi M là giá trị lớn nhất của hàm số \(\begin{equation} f(x)=\left|3 x^{4}-4 x^{3}-12 x^{2}+m\right| \end{equation}\) trên đoạn [-1;3]. Có bao nhiêu số thực m để \(\begin{equation} M=\frac{59}{2} ? \end{equation}\)
   

• Hàm số \(y=\cos 2 x-4 \sin x+4\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) lần lượt là:

• Cho \(x^{2}-x y+y^{2}=2 \text { . }\)Giá trị nhỏ nhất của \(P=x^{2}+x y+y^{2} b\) bằng 

• Xét hàm số \(y = \left| {{x^2} + ax + b} \right|\), với a,b là tham số. Gọi M là giá trị lớn nhất của hàm số trên \(\left[ { – 1;3} \right]\). Khi M nhận giá trị nhỏ nhất có thể được, tính a + 2b.

• Giá trị lớn nhất của hàm số \(y=2 \sin ^{2} x-\cos x\) là phân số tối giản có dạng với a, b là các số nguyên dương. Tìm a-b?

• Tìm giá trị lớn nhất của hàm số \(f(x)=\frac{x^{2}-3 x+6}{x-1}\) trên [2;4]

• Cho hàm số \(f\left( x \right) = \frac{{x – {m^2}}}{{x + 8}}\) với m là tham số thực. Giả sử \({m_0}\) là giá trị dương của tham số m để hàm số có giá trị nhỏ nhất trên đoạn \(\left[ {0;3} \right]\) bằng – 3. Giá trị \({m_0}\) thuộc khoảng nào trong các khoảng cho dưới đây?

• Giá trị nhỏ nhất của hàm số \(f(x)=x+\frac{1}{x}\) trên nửa khoảng \([2 ;+\infty)\) là?

• M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = x + 1 + \sqrt {2 – {x^2}} \). Tính M – m?

• Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\sqrt{x-1}+\sqrt{7-x} .\) . Khi đó
  có bao nhiêu số nguyên dương nằm giữa m và M ? 

• Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^4} – 2{x^2} + 3\) trên đoạn \(\left[ {0;2} \right]\). Tổng M + m bằng