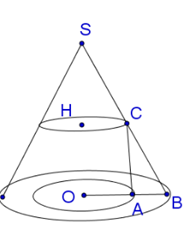
Cho hình chóp đều \(S.ABC\) có đường cao \(SH=a\); góc \(SAB\) bằng 45 độ. Bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD
Khi đó IA = IB = IC = ID = IS hay \(\left\{ \begin{array}{l} IA = IB = IC = ID(1)\\ IA = IS(2) \end{array} \right.\)
Gọi H là giao điểm của AC và \(BD.\) Từ (1) suy ra \(I\in SH(*)\)
Trong mặt phẳng (SAH) dựng đường thẳng \(\Delta \) là trung trực của \(SA.\)
Từ (2), suy ra
\(\begin{array}{l} I \in \Delta (2*)\\ (*) + (2*) \to SH \cap \Delta = \left\{ I \right\} \end{array}\)
Gọi M là trung điểm của SA, khi đó:
\(\frac{SI}{SA}=\frac{SM}{SH}\to R=SI=\frac{SM.SA}{SH}=\frac{SA.SA.}{2SH}=\frac{S{{A}^{2}}}{2SH}\).Do SAB cân tại S và có \(\angle SAB={{45}^{0}}\) nên SAB vuông cân tại S. Đặt \(SA=x\), khi đó \(AB=x\sqrt{2};HA=\frac{AB\sqrt{3}}{3}=\frac{x\sqrt{6}}{3}\)
Trong tam giác vuông SHA có:\(S{{A}^{2}}-H{{A}^{2}}=S{{H}^{2}}\leftrightarrow {{x}^{2}}-\frac{6{{x}^{2}}}{9}={{a}^{2}}\leftrightarrow {{x}^{2}}=3{{a}^{2}}\to R=\frac{3{{a}^{2}}}{2a}=\frac{3a}{2}\)
Câu hỏi liên quan
-
Trong không gian với hệ tọa độ Oxyz. Phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( {2\,;\,0\,;\,1} \right)\) và tiếp xúc với đường thẳng \(d:\frac{{x – 1}}{1} = \frac{y}{2} = \frac{{z – 2}}{1}\) là
-
Một hình hộp chữ nhật có ba kích thước lần lượt là a,b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a,b,c là:
-
Cho mặt cầu \(\left( S \right)\) Có tâm \(I\), bán kính \(R=5\). Một đường thằng \(\Delta \) cắt \(\left( S \right)\) tại \(2\) điểm \(M\), \(N\) phân biệt nhưng không đi qua \(I\). Đặt \(MN=2m\). Với giá trị nào của m thì diện tích tam giác \(IMN\) lớn nhất?
-
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B có cạnh AB = 3 , BC = 4 và góc giữa DC và mặt phẳng (ABC) bằng 450. Tính thể tích mặt cầu ngoại tiếp tứ diện.
-
Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4. Tổng độ dài đường kính của hai quả bóng đó.
-
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x – 2y – 2z – 8 = 0\). Phương trình mặt cầu tâm \(I\left( {1;2; – 1} \right)\) và tiếp xúc với mặt phẳng \(\left( P \right)\) là
-
Cho tứ diện \(ABCD\) có \(ABC\) và \(ABD\) là các tam giác đều cạnh a và nằm trong hai mặt phẳng vuông góc với nhau. Tính diện tích mặt cầu ngoại tiếp tứ diện \(ABCD\) theo \(a.\)
-
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có tâm I (-1;4;2) và tiếp xúc mặt phẳng \((P):-2 x+2 y+z+15=0 \text { . }\) . Khi đó phương trình của mặt cầu (S) là
-
Cho mặt cầu có diện tích bằng \(\frac{{8\pi {a^2}}}{3}\). Khi đó bán kính mặt cầu bằng.
-
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h;OB=R;OH=x0<x<h. Tìm thể tích lớn nhất của hình trụ.
-
Diện tích S của mặt cầu có bán kính \(R = a\sqrt 5 \) là
-
Trong không gian với hệ tọa độ Oxyz , mặt cầu tâm \(I(2 ;-1 ; 3\) tiếp xúc với mặt phẳng (Oxy) có phương trình
-
Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:
-
Mặt cầu tâm \(I\left( { – 1;2;0} \right)\) đường kính bằng 10 có phương trình là:
-
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt cầu tâm \(I\left( {1;\,2;\, – 4} \right)\) và thể tích của khối cầu tương ứng bằng \(36\pi \)?
-
Trong không gian với hệ trục tọa độ Oxyz, mặt cầu \(\left( S \right):{\left( {x + 2} \right)^2} + {\left( {y – 1} \right)^2} + {z^2} = 4\) có tâm I và bán kính R lần lượt là
-
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \(A\left( {0;{\rm{ }}1;{\rm{ }}1} \right), B\left( {3;{\rm{ }}0; – 1} \right), C\left( {0;{\rm{ }}21; – 19} \right)\) và mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 1} \right)^2} = 1\). \(M\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\) là điểm thuộc mặt cầu \(\left( S \right)\) sao cho biểu thức \(T = 3M{A^2} + 2M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất. Tính tổng a + b + c.
-
Phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và tiếp xúc với mặt phẳng \(\left( {Oyz} \right)\) là
-
Mặt cầu \(\left( S \right)\) tâm \(I\left( {1;2;4} \right)\) và tiếp xúc với mặt cầu \(\left( {{S_1}} \right):{(x + 1)^2} + {y^2} + {(z – 2)^2} = 27\) có phương trình:
-
Cho \(I\left( {1; – 2;3} \right)\). Viết phương trình mặt cầu tâm I cắt trục Ox tại hai điểm A và B sao cho \(AB = 2\sqrt 3 \).
