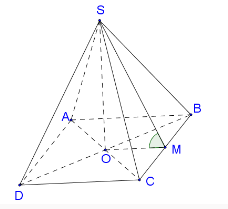
Cho hình chóp đều S.ABCD có AC = 2a, mặt bên (SBC) tạo với mặt đáy (ABCD) một góc 450 . Tính thể tích V của khối chóp S.ABCD.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiGọi x là độ dài cạnh góc vuông\( \Rightarrow {x^2} + {x^2} = 4{a^2} \Rightarrow x = a\sqrt 2 \Rightarrow OM = \frac{{a\sqrt 2 }}{2}\)
Ta có: \( SO = OM.\tan {45^0} = \frac{{a\sqrt 2 }}{2}\)
Vậy: \( V = \frac{1}{3}.2{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{3}.\)
ADMICRO
YOMEDIA
ZUNIA9