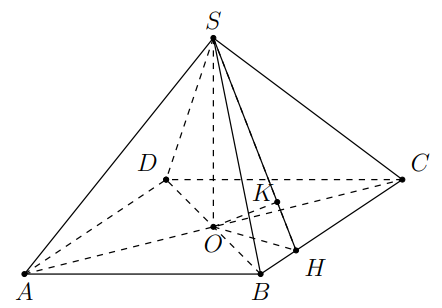
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc \(\widehat{B A D}=60^o\) , có SO vuông góc với mặt đáy và SO = a. Khoảng cách từ O đến mặt phẳng (SBC) là

A. \(\begin{array}{llll} \frac{a \sqrt{57}}{19} \end{array}\)

B. \(\frac{a \sqrt{57}}{18} \)

C. \(\frac{a \sqrt{45}}{7}\)

D. \(\frac{a \sqrt{52}}{16} .\)

Sai A là đáp án đúng Xem lời giải

Chính xác Xem lời giải

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

ATNETWORK

Môn: Toán Lớp 11

Chủ đề: Quan hệ vuông góc trong không gian

Bài: Khoảng cách

Lời giải:

Báo sai

Gọi H là hình chiếu của O trên BC, K là hình chiếu của O trên SH. Khi đó ta có OK ⊥ (SBC) hay d(O,(SBC)) = OK. Ta có

\(\frac{1}{O K^{2}}=\frac{1}{S O^{2}}+\frac{1}{O H^{2}}=\frac{1}{S O^{2}}+\frac{1}{O B^{2}}+\frac{1}{O C^{2}}\)

\(\text { Do } \widehat{B A D}=60^{\circ} \text { nên } \widehat{O B C}=60^{\circ}, \text { suy ra } O B=\frac{a}{2} \text { , }O C=\frac{a \sqrt{3}}{2} \text { . }\)

Thay vào đẳng thức trên ta được \(OK=\frac{a \sqrt{57}}{19}\)

ADMICRO

YOMEDIA

Câu hỏi liên quan

Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh \(a\) . Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết thể tích của khối lăng trụ là \(\frac{{{a}^{3}}\sqrt{3}}{4}\). Tính khoảng cách giữa hai đường thẳng AA’ và BC.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4, AD = 3. Mặt phẳng (ACD') tạo với mặt đáy một góc 60^O. Tính khoảng cách giữa hai mặt đáy của hình hộp.
Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\), đáy ABCD là hình chữ nhật với \(AC = a\sqrt 5 \) và \(BC = a\sqrt 2 \). Tính khoảng cách giữa SD và BC.

ZUNIA12

Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng \(\sqrt{2}a\). Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \(\frac{4}{3}{{a}^{3}}\). Khoảng cách h từ B đến mặt phẳng (SCD) là:
Cho lăng trụ tam giác \(ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\) có tất cả các cạnh bằng a, góc tại bởi cạnh bên và mặt phẳng đáy bằng \({{30}^{0}}\). Hình chiếu H của điểm A trên mặt phẳng \(\left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\)thuộc đường thẳng \({{B}_{1}}{{C}_{1}}\). Khoảng cách giữa hai đường thẳng \(A{{A}_{1}}\) và \({{B}_{1}}{{C}_{1}}\) theo a bằng:
Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a. Khoảng cách từ A đến mặt phẳng \(\left( {SBC} \right)\) bằng
Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Tính khoảng cách giữa đường thẳng MN và (ABC).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45⁰. Tính khoảng cách giữa hai đường thẳng SB, AC.
Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN và (ABC) bằng:
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 2 và cạnh bên bằng 3 (tham khảo hình bên). Tính khoảng cách từ S đến mặt phẳng \(\left( {ABCD} \right)\).
Cho tứ diện O.ABC có OA,OB,OC đôi một vuông góc với nhau \(OA = OB = OC = \sqrt 3 .\) Khoảng cách từ O đến \(mp(ABC)\) là
Hình chóp có đáy là tam giác vuông tại B, BA = 3a, BC=4a, (SBC) vuông góc với đáy. Biết SB = 2a\(\sqrt3\), góc SBC = 30^o. Tính khoảng cách từ B đến (SAC)
Xét tứ diện (OABC ) có (OA ), (OB ), (OC ) đôi một vuông góc. Gọi \(\alpha, \beta, \gamma \) lần lượt là góc giữa các đường thẳng (OA ), (OB ), (OC ) với mặt phẳng (ABC) (hình vẽ).

Khi đó giá trị nhỏ nhất của biểu thức \( M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a, H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (AB'C) và (A'DC') bằng:
Cho hình chóp SABC, \(\Delta SAB\) đều cạnh a nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ C đến mặt phẳng \(\left( {SAB} \right)\) biết \(V = \frac{{{a^3}\sqrt 3 }}{6}\).
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác đều cạnh a. Góc giữa \(CA'\) và mặt \((AA'B'B)\) bằng \(30{}^\circ \). Gọi d(AI’,AC) là khoảng cách giữa \(A'I\) và AC, kết quả tính d(AI’,AC) theo a với I là trung điểm AB là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết \(BC=a\sqrt{3}\), \(BA=a\). Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AC và biết thể tích khối chóp S.ABC bằng\(\frac{{{a}^{3}}\sqrt{6}}{6}\). Khoảng cách h từ C đến mặt phẳng (SAB) là.
Cho hình chóp S.ABC có AS, AB, AC đôi một vuông góc với nhau, \(AB=a,AC=a\sqrt{2}\). Tính khoảng cách d từ đường thẳng SA đến BC
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm H của cạnh AB. Góc tạo bởi SC và (ABCD) bằng 45⁰. Tính theo a tính khoảng cách giữa hai đường thẳng SD và AB.