Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), cạnh \(SB\) vuông góc với đáy và mặt phẳng \(\left( SAD \right)\) tạo với đáy một góc \({{60}^{{}^\circ }}\). Tính thể tích khối chóp \(S.ABCD\).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai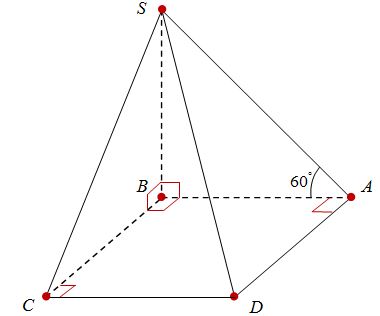
Ta có: \(\left. \begin{array}{l} SB \bot \left( {ABCD} \right)\\ AD \subset \left( {ABCD} \right) \end{array} \right\} \Rightarrow SB \bot AD\) mà \(AD\bot AB\Rightarrow AD\bot SA\).
\(\left. \begin{array}{l} \left( {SAD} \right) \cap \left( {ABCD} \right) = AD\\ AB \bot AD,AB \subset \left( {ABCD} \right)\\ SA \bot AD,SA \subset \left( {SAD} \right) \end{array} \right\} \Rightarrow \) \(\left( \left( SAD \right);\left( ABCD \right) \right)=\left( SA;AB \right)=\widehat{SAB}={{60}^{{}^\circ }}\)
Ta có: \(SB=BD.\tan {{60}^{{}^\circ }}=2a\sqrt{3}\).
Vậy \(V=\frac{1}{3}SB.{{S}_{ABCD}}=\frac{1}{3}2a\sqrt{3}.4{{a}^{2}}=\frac{8{{a}^{3}}\sqrt{3}}{3}\).











