Cho hình chóp S.ABCD có đáy là hình vuông. Cạnh bên SA vuông góc với mặt phẳng đáy và SA=a . Diện tích tam giác SBC bằng \(\frac{a^{2} \sqrt{2}}{2}\) Thể tích khối chóp đã cho bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai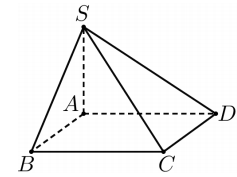
Đặt cạnh hình vuông là x >0.
Suy ra \(S B=\sqrt{S A^{2}+A B^{2}}=\sqrt{a^{2}+x^{2}}\)
Dễ thấy \(B C \perp(S A B) \Rightarrow B C \perp S B\) nên ta có
\(\frac{a^{2} \sqrt{2}}{2}=S_{\Delta A B C}=\frac{1}{2} S B \cdot B C=\frac{1}{2} \sqrt{a^{2}+x^{2}} \cdot x \longrightarrow x=a\)
Vậy thể tích khối chóp \(V_{s . A B C D}=\frac{1}{3} S_{A B C D} \cdot S A=\frac{a^{3}}{3}\)
ADMICRO
YOMEDIA
ZUNIA9











