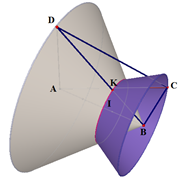
Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \( SA = \frac{{2a\sqrt 3 }}{3}\) . Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABD
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDo D đối xứng với C qua B nên có BC=DC=AC suy ra tam giác ABD là tam giác vuông tại A.
Kẻ đường thẳng dd qua C vuông góc với đáy, đường thẳng này là trục đường tròn ngoại tiếp tam giác đáy ABD .
Tam giác SAB cân tại S , gọi M là trung điểm AB,H là tâm đường tròn ngoại tiếp tam giác SAB
\(\begin{array}{l} \Rightarrow H \in SM;SM = \sqrt {S{A^2} - A{M^2}} = \frac{{a\sqrt {13} }}{{2\sqrt 3 }}\\ SH = \frac{{AB.SA.SB}}{{4.{S_{SAB}}}} = \frac{{{{\left( {\frac{{2a}}{{\sqrt 3 }}} \right)}^2}.a}}{{4.\frac{1}{2}.a.AM}} = \frac{{4a}}{{\sqrt {39} }} \end{array}\)
Trong (SAC) dựng HI⊥SM (I∈d) (1).
Mà \(\left\{ \begin{array}{l} AB \bot SM\\ AB \bot MC \end{array} \right. \to AB \bot (SMC) \to AB \bot HI(2)\)
Từ (1), (2) suy ra HI⊥(SAB) , suy ra II là tâm đường tròn ngoại tiếp hình chóp S.ABD
Gọi Q=MS∩CI, xét tam giác SCM có
\(\begin{array}{l} \frac{{SM}}{{QM}} = \frac{{MG}}{{MC}} = \frac{1}{3} \Rightarrow QM = 3SM = 3.\frac{{a\sqrt {13} }}{{2\sqrt 3 }} = \frac{{a\sqrt {39} }}{2}\\ \Rightarrow QH = QM - MS + HS = \frac{{a\sqrt {39} }}{2} - \frac{{a\sqrt {13} }}{{2\sqrt 3 }} + \frac{{4a}}{{\sqrt {39} }} = \frac{{17a}}{{\sqrt {39} }}\\ QC = \sqrt {Q{M^2} - M{C^2}} = 3a \end{array}\)
Xét: \(\begin{array}{l} {\rm{\Delta }}QHI \sim {\rm{\Delta }}QCM \Rightarrow \frac{{HI}}{{CM}} = \frac{{HQ}}{{QC}} \Rightarrow HI = \frac{{HQ.CM}}{{QC}} = \frac{{17a}}{{6\sqrt {13} }}\\ \Rightarrow R = SI = \sqrt {H{I^2} + H{S^2}} = \sqrt {{{\left( {\frac{{a\sqrt {17} }}{{6\sqrt {13} }}} \right)}^2} + {{\left( {\frac{{4a}}{{\sqrt {39} }}} \right)}^2}} = \frac{{a\sqrt {37} }}{6} \end{array}\)
.PNG)