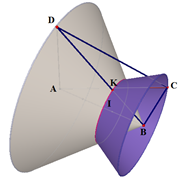
Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Tập hợp các điểm \(M\) sao cho \(M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}+M{{D}^{2}}=2{{a}^{2}}\) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi \(I,J\) lần lượt là trung điểm của \(AB,\ CD\). Gọi \(K\) là trung điểm \(IJ\). (Lúc này, \(K\) là trọng tâm tứ diện).
Áp dụng định lý đường trung tuyến trong tam giác, ta có:
\(\left\{ \begin{array}{l} M{A^2} + M{B^2} = 2M{I^2} + \frac{{A{B^2}}}{2} = 2M{I^2} + \frac{{{a^2}}}{2}\\ M{C^2} + M{D^2} = 2M{J^2} + \frac{{C{D^2}}}{2} = 2M{J^2} + \frac{{{a^2}}}{2} \end{array} \right.\)
\(\Rightarrow M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}+M{{D}^{2}}=2\left( M{{I}^{2}}+M{{J}^{2}} \right)+{{a}^{2}}\) \)=2\left( 2M{{K}^{2}}+\frac{I{{J}^{2}}}{2} \right)+{{a}^{2}}\)
Ta có: \(I{{J}^{2}}=\frac{I{{C}^{2}}+ID{}^{2}}{2}-\frac{C{{D}^{2}}}{4}=I{{C}^{2}}-\frac{{{a}^{2}}}{4}={{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}-\frac{{{a}^{2}}}{4}=\frac{{{a}^{2}}}{2}\)
\(\Rightarrow M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}+M{{D}^{2}}=4M{{K}^{2}}+\frac{3{{a}^{2}}}{2}\).
Do đó: \(M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}+M{{D}^{2}}=2{{a}^{2}}\Leftrightarrow 4M{{K}^{2}}+\frac{3{{a}^{2}}}{2}=2{{a}^{2}}\Leftrightarrow MK=\frac{a\sqrt{2}}{4}\).
Vậy tập hợp các điểm \(M\) thoả mãn hệ thức đề bài là mặt cầu tâm \(K\), bán kính bằng \(\frac{a\sqrt{2}}{4}\).