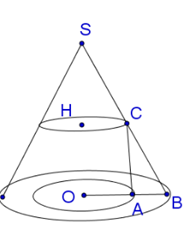
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\), cạnh huyền \(BC=6\,\,\left( cm \right)\), các cạnh bên cùng tạo với đáy một góc \(60{}^\circ \). Diện tích mặt cầu ngoại tiếp hình chóp \(S.ABC\) là

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và \(AB = 2, AC = 4,SA = \sqrt5\)Mặt cầu đi qua các đỉnh của hình chóp (S.ABC ) có bán kính là

Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0;1;2) và B(2;−1;4). Phương trình mặt cầu đường kính AB là

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B có cạnh AB = 3 , BC = 4 và góc giữa DC và mặt phẳng (ABC) bằng 45⁰. Tính thể tích mặt cầu ngoại tiếp tứ diện.

Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x + 4y – 4z – m = 0\) có bán kính R = 5. Giá trị của tham số m bằng

Cho khối cầu có thể tích là \(36\pi\) . Diện tích mặt cầu đã cho bằng

Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;3; 2) và mặt phẳng \((P): 3 x+6 y-2 z-4=0\). Phương trình mặt cầu tâm A, tiếp xúc với mặt phẳng (P) là 

Tính bán kính r của khối cầu có thể tích là \(V = 36\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\)

Diện tích mặt cầu có bán kính \(R\) là

Trong không gian với hệ trục Oxyz, cho mặt cầu \(\left( S \right)\) có tâm \(I\left( {0; – 2;1} \right)\) và mặt phẳng \(\left( P \right):x + 2y – 2z + 3 = 0\). Biết mặt phẳng \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là một đường tròn có diện tích là \(2\pi \). Phương trình mặt cầu \(\left( S \right)\) là

Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai mặt cầu \(\left( {{S_1}} \right):{x^2} + {y^2} + {z^2} = 1,\left( {{S_2}} \right):{x^2} + {\left( {y – 4} \right)^2} + {z^2} = 4\) và các điểm \(A\left( {4;0;0} \right), B\left( {\frac{1}{4};0;0} \right), C\left( {1;4;0} \right), D\left( {4;4;0} \right)\). Gọi M là điểm thay đổi trên \(\left( {{S_1}} \right)\), N là điểm thay đổi trên \(\left( {{S_2}} \right)\). Giá trị nhỏ nhất của biểu thức Q = MA + 2ND + 4MN + 4BC là

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Cho ba hình cầu có bán kính lần lượt là R₁, R₂ ,R₃ đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài cạnh lần lượt là 2, 3, 4. Tính tổng \(R_1 + R_2 + R_3\)

Một hình hộp chữ nhật có độ dài ba cạnh lần lượt là 2;2;1. Tìm bán kính R của mặt cầu ngoại tiếp hình hộp chữ nhật trên.

Cho hình chóp S.ABCD có đáy là hình vuông cạnh \(2\sqrt2\). Cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3 Mặt phẳng \((\alpha)\) qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại M, N, P . Thể tích V của khối cầu ngoại tiếp tứ diện CMNP

Trục đa giác đáy là đường thẳng vuông góc với mặt phẳng đáy tại:

Cho mặt cầu tâm O bán kính R và điểm A bất kì trong không gian. Điểm A không nằm ngoài mặt cầu khi và chỉ khi:

Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5 ,cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 ,cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 ,cm. Bán kính của viên billiards đó bằng

Cho mặt cầu \(S\left( O;R \right),A\) là một điểm ở trên mặt cầu \(\left( S \right)\) và \(\left( P \right)\) là mặt phẳng đi qua A sao cho góc giữa OA và (P) bằng \({{60}^{0}}.\) Diện tích của đường tròn giao tuyến bằng:

Cho mặt cầu \(\left( S \right)\) tâm O, bán kính R và mặt phẳng \(\left( P \right)\) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt \(\left( P \right)\) tại N. Hình chiếu của O trên \(\left( P \right)\) là I. Mệnh đề nào sau đây là đúng?

Cho hình chóp \(S.ABC\)có \(SA\)vuông góc với mặt phẳng \(\left( ABC \right),\,\,SA=a,\,\,AB=a\),\(AC=2a,\) \(\widehat{BAC}={{60}^{0}}.\) Tính diện tích hình cầu ngoại tiếp hình chóp \(S.ABC\).