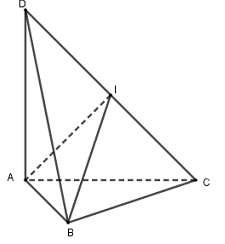
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B có cạnh AB = 3 , BC = 4 và góc giữa DC và mặt phẳng (ABC) bằng 450. Tính thể tích mặt cầu ngoại tiếp tứ diện.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có :
\(\left\{ \begin{array}{l} BC \bot BA\\ BC \bot DA \end{array} \right. \to BC \bot (ABD) \to BC \bot BD\) ⇒ ΔBCD vuông tại B.
Gọi I là trung điểm của CD thì \( IB = IC = ID = \frac{1}{2}CD\)
Do đó \(IA=IB=IC=ID⇒\) I là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Tam giác ABC vuông tại B nên \( AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {4^2}} = 5\) (Định lí Pytago).
Vì DA⊥(ABC) nên AC là hình chiếu của DC lên (ABC).
\( \Rightarrow \angle \left( {DC;\left( {ABC} \right)} \right) = \angle \left( {DC;AC} \right) = \angle DCA = {45^0}\)
Tam giác DAC vuông tại A có \( \widehat {DCA} = {45^0}\) nên là tam giác vuông cân \(\begin{array}{l} \Rightarrow DC = AC\sqrt 2 = 5\sqrt 2 \\ \Rightarrow R = IA = \frac{1}{2}DC = \frac{{5\sqrt 2 }}{2} \end{array}\)
Vậy thể tích khối cầu ngoại tiếp tứ diện ABCD là :
\( V = \frac{4}{3}\pi I{A^3} = \frac{4}{3}\pi .{\left( {\frac{{5\sqrt 2 }}{2}} \right)^3} = \frac{{125\sqrt 2 }}{3}\pi \)