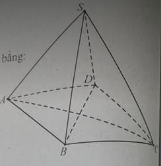
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh AB=a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60o. Tính theo a thể tích tứ diện B’ABC và khoảng cách từ B đến mặt phẳng (AB’C).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Theo như đề bài dữ kiện thì ta có thể dễ dàng tính được thể tích của khối lăng trụ tam giác đều ban đầu, từ đó suy ra thể tích của khối tứ diện AB’BC. Để tính được khoảng cách từ B đến (AB’C) thực chất là tìm chiều cao của tứ diện, đến đây bài toán sẽ được giải quyết nếu quý độc giả tìm được diện tích tam giác AB’C.
Vì đề bài cho dữ kiện ((A’BC), (ABC))=60o, nên ta sẽ đi xác định góc này bằng cách gọi H là trung điểm của BC. Tam giác ABC đều nên AH\(\bot \)BC (1).
A’A\(\bot \)(ABC) ⟹A’A\(\bot \)BC (2)
Từ (1) và (2) ⟹BC\(\bot \)A’H ⟹((A’BC), (ABC)) = A’HA = 60o
⟹A’A = AH.tan 60o=\(\frac{3a}{2}\). Khi đó \({{V}_{ABC.A'B'C'}}=A'A.{{S}_{ABC}}=\frac{3a}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3{{a}^{3}}\sqrt{3}}{8}\)
Và \({{V}_{B'ABC}}=\frac{1}{3}V=\frac{{{a}^{3}}\sqrt{3}}{8}\) lúc này ta có thể loại C và D.
Dễ thấy diện tích tam giác AB’C có thể được do B’AC cân tại B’ có
\(B'A=B'C=\sqrt{{{a}^{2}}+{{\left( \frac{3a}{2} \right)}^{2}}}=\frac{a\sqrt{13}}{2};AC=a\)
Dễ tính được chiều cao kẻ từ B’ của tam giác có độ dài là \(a\sqrt{3}\)
\(\Rightarrow {{S}_{ACB'}}=\frac{{{a}^{2}}\sqrt{3}}{2}\Rightarrow d(B;(AB'C))=\frac{3{{V}_{{{B}_{ABC}}}}}{{{S}_{AB'C}}}=\frac{3a}{4}\)