Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi O’, O là tâm của hai hình vuông ABCD và \(A'B'C'D'\) và \(O'O=a.\) Gọi \({{V}_{1}}\) là thể tích của hình trụ tròn xoay đáy là hai đường tròn ngoại tiếp các hình vuông \(ABCD,A'B'C'D'\) và \({{V}_{2}}\) là thể tích hình nón tròn xoay đỉnh O’ và đáy là đường tròn nội tiếp hình vuông \(ABCD.\) Tỉ số thể tích \(\frac{{{V}_{1}}}{{{V}_{2}}}\) là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai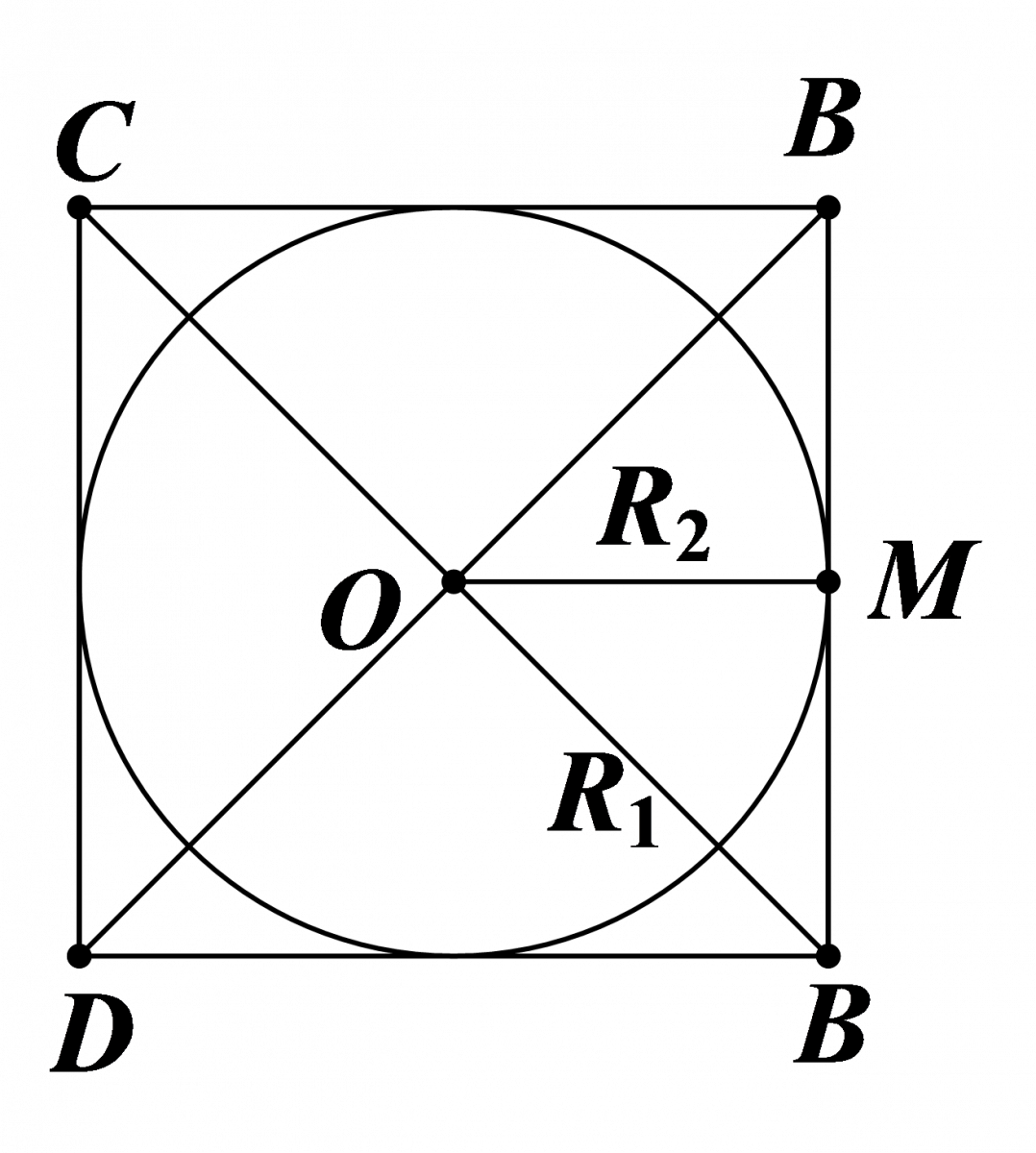
Gọi M trung điểm của AB thì tam giác OAM vuông cân tại M.
\({{R}_{1}}=OA=\frac{\sqrt{2}}{2}\,\,;\,\,\,{{R}_{2}}=OM=\frac{1}{2}\)
\(\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\pi R_{1}^{2}.h}{\frac{1}{3}\pi R_{2}^{2}.h}=3{{\left( \frac{\sqrt{2}}{2} \right)}^{2}}:\left( \frac{1}{4} \right)=6\)
ADMICRO
YOMEDIA
ZUNIA9
.png)











