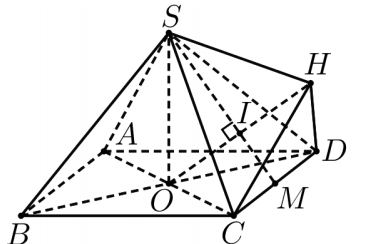
Cho khối chóp tứ giác đều S.ABCD . có đáy là hình vuông tâm O, cạnh bằng a. Cạnh bên bằng \(a \sqrt{3}\). Gọi M là trung điểm của CD, H là điểm đối xứng của O qua SM (tham khảo hình vẽ bên). Thể tích khối đa diện ABCDSH bằng

Câu hỏi liên quan

• Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và SA = 2a. Tính thể tích khối chóp S.ABC.

• Cho khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \), khoảng cách giữa hai đáy của lăng trụ bằng \(a\sqrt 6 \). Tính thể tích V của khối lăng trụ

• Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Tính thể tích khối tứ diện OABC.

ZUNIA12

• Cho hình thang vuông ABCD có đường cao AD = 1 , đáy nhỏ AB = 1, đáy lớn CD = 2. Cho hình thang đó quay quanh AB ta được khối tròn xoay có thể tích bằng

• Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh 2a và A’B = 3a. Tính thể tích khối hộp chữ nhật ABCD.A’B’C’D’ theo a.

• Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có AB = a, AD = 3a, BC = a. Biết SA = \(a\sqrt 3 \), tính thể tích khối chóp S.BCD theo a.

• Cho khối chóp S ABC . có đáy là tam giác vuông tại B, \(A B=a, \quad A C=2 a\)2 . Cạnh bên SA vuông góc với mặt phẳng đáy và S A=a. Thể tích của khối chóp đã cho bằng

• Cho hình chóp S.ABC có SA=a và vuông góc với đáy ABC. Biết rằng tam giác ABC  đều và mặt phẳng \(\left( SBC \right)\) hợp với đáy \(\left( ABC \right)\) một góc \(30{}^\circ \). Tính thể tích \(V\) của khối chóp S.ABC.

• Cho hình chóp S.ABC có đáy là tam giác vuông tại C, \(AB = a\sqrt 5 \), AC = a. Cạnh bên SA = 3a và vuông góc với mặt phẳng (ABC). Thể tích khối chóp S.ABC bằng:

• Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\), \(AB=a\), \(AC=2a\). Hình chiếu vuông góc của \(S\) lên \(\left( ABC \right)\) là trung điểm \(M\) của \(AC\). Góc giữa \(SB\) và đáy bằng \(60{}^\circ \). Thể tích \(S.ABC\) là bao nhiêu?

• Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và mặt đáy bằng 30⁰. Tính thể tích của lăng trụ đã cho theo a.

• Cho hình hộp chữ nhật \(ABCD.{A}'{B}'{C}'{D}'\) có đáy là hình vuông, cạnh bên bằng  \(4a\)  và đường chéo \(5a\) .Tính thể tích hình hộp chữ nhật này.

• Cho khối hộp chữ nhật ABCDA'B'C'D'  có \(A A^{\prime}=a, A B=3 a, A C=5 a\)  . Thể tích của khối hộp đã cho bằng

• Nếu tăng chiều dài hai cạnh đáy của khối hộp chữ nhật lên 10 lần thì thể tích tăng lên bao nhiêu lần?

• Cho hình chóp tam giác S.ABC có \(SA = SB = SC = a\sqrt 2 \), tam giác ABC vuông cân tại A và BC = 2a. Tính thể tích V của khối chóp S.ABC.

• Cho khối tự diện OABC có OA, OB, OC đôi một vuông góc và OA = a; OB = b; OC = c. Thể tích khối tứ diện OABC được tính theo công thức nào sau đây

• Gọi V là thể tích của hình lập phương ABCD.A’B’C’D’, \({V_1}\) là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng?

• Cho khối chóp S.ABC. Trên các đoạn SA, SB, SC lần lượt lấy ba điểm A', B', C’ sao cho \(SA'=\frac{1}{2}SA;SB'=\frac{1}{3}SB;SC'=\frac{1}{4}SC\). Khi đó tỉ số thể tích của hai khối chóp S.A'B'C' và S.ABC bằng:

• Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần

• Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc \(\widehat{S B D}=60^{\circ}\).Thể tích khối chóp đã cho bằng