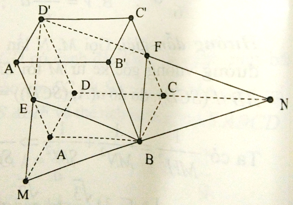
Cho khối hộp đứng \(ABCD.A'B'C'D'\) có \(AB=a,AD=b,\widehat{BAD}=\alpha ;\) đường chéo \(AC'\) hợp với đáy góc \(\beta .\) Tính thể tích khối hộp đứng đã cho là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
\(V=ab\sqrt{{{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\alpha }.\sin \alpha .\tan \beta \)
Ta có: \(CC'\bot \left( ABCD \right)\)
\(\Rightarrow \overset\frown{CAC'}=\beta \) là góc của \(AC'\) và mặt đáy \(\left( ABCD \right)\) .
Xét \(\Delta ABC\) , ta có: \(A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2AB.BC.c\text{os}\widehat{ABC}\)
\(={{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\left( {{180}^{0}}-\alpha \right)={{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\alpha .\)
\(\Rightarrow AC=\sqrt{{{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\alpha }\)
Do đó ta có: \(CC'=AC.\tan \beta =\sqrt{{{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\alpha }.\tan \beta \) .
Thể tích của hình hộp đứng: \(V={{S}_{ABCD}}.CC'=ab\sin \alpha .\sqrt{{{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\alpha }.\tan \beta \)
\(V=ab\sqrt{{{a}^{2}}+{{b}^{2}}+2ab.c\text{os}\alpha }.\sin \alpha \text{.tan}\beta \)
Câu hỏi liên quan
-
Thể tích của khối có 5 mặt hình chữ nhật, 4 mặt tam giác với kích thước được cho như hình vẽ là
.png)
-
Một khối chóp có chiều cao bằng 2, diện tích đáy bằng 6. Tính thể tích khối chóp đã cho.
-
Cho hình lập phương ABCD.A’B’C’D’ có diện tích mặt chéo ACC’A’ bằng \(2\sqrt{2}{{a}^{2}}\). Thể tích của khối lập phương ABCD.A'B'C'D' là:
-
Cho hình chóp S.ABC có \( SA = SB = SC = a\sqrt 3 ;AB = AC = a;BC = 3a\). Thể tích khối chóp S.ABC bằng:
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.
-
Đường chéo của một hình hộp chữ nhật bằng d, góc giữa đường chéo và mặt đáy là \(\alpha \), góc nhọn giữa hai đường chéo của đáy bằng \(\beta \). Thể tích của hình hộp đó là:
-
Cho hình chóp S.ABCD có đáy là hình bình hành, gọi M là trung điểm của SC, mặt phẳng đi qua AM và song song với BD cắt SB, SD lần lượt tại N và P. Tính tỉ số k giữa thể tích hình chóp S.ANMP và thể tích hình chóp S.ABCD.
-
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đáy; BC=9m,AB=10m,AC=17m. Biết thể tích khối chóp S.ABC bằng 73m3 Tính khoảng cách h từ điểm A đến mặt phẳng (SBC).
-
Thể tích của khối lập phương ABCD.A’B’C’D’ với AD’ = 3a.
-
Cho hình lập phương có cạnh bằng 1. Diện tích của mặt cầu ngoại tiếp hình lập phương đó bằng
-
Thể tích của khối chóp có chiều cao 2a và diện tích đáy bằng \(3{a^2}\) là:
-
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, \(AB = a\sqrt 5 \), AC = a. Cạnh bên SA = 3a và vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính thể tích khối chóp S.ABC.
-
Cho khối tứ diện \(OABC\) với \(OA,\,\,OB,\,\,OC\) vuông góc từng đôi một và \(OA=a,\text{ }OB=2a,\text{ }OC=3a.\) Gọi M, N lần lượt là trung điểm của hai cạnh \(AC,\,\,BC.\) Thể tích của khối tứ diện \(OCMN\) tính theo a bằng:
-
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và SA = 2a. Thể tích khối chóp S.ABCD bằng
-
Cho hình chóp \(S.ABC\) có mặt phẳng \(\left( SAC \right)\) vuông góc với mặt phẳng \(\left( ABC \right)\), \(SAB\) là tam giác đều cạnh \(a\sqrt{3}\), \(BC=a\sqrt{3}\) đường thẳng \(SC\) tạo với mặt phẳng \(\left( ABC \right)\) góc \(60{}^\circ \). Thể tích của khối chóp \(S.ABC\) bằng
-
Cho lăng trụ đều ABC.EFH có tất cả các cạnh bằng a. Gọi S là điểm đối xứng của A qua BH. Thể tích khối đa diện ABCSFH bằng
-
Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
-
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật, tam giác \(SAD\) vuông tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Cho biết AB=a, \(SA=2SD\). Mặt phẳng \(\left( SBC \right)\) tạo với đáy một góc \({{60}^{\text{o}}}\). Thể tích khối chóp \(S.ABCD\) là
-
Thể tích V của khối lăng trụ có diện tích đáy bằng 3 và độ dài đường cao bằng 4 là
-
Cho hình chóp S ABCD . có đáy là hình vuông tâm O, BD =1. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt phẳng đáy một góc 600 Thể tích của khối chóp đã cho bằng
