Cho lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, biết \(A^{\prime} O=a\) . Thể tích của khối lăng trụ đã cho bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai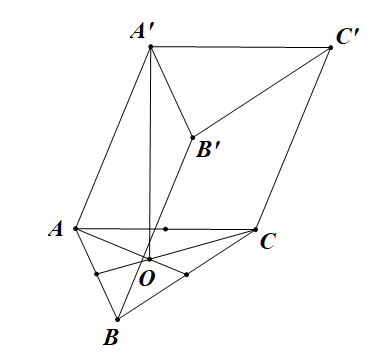
Chiều cao khối lăng trụ:\(A^{\prime} O=a\) .
Diện tích tam giác đều: \(S_{\Delta A B C}=\frac{a^{2} \sqrt{3}}{4}\)
Vậy thể tích khối lăng trụ \(V_{A B C, A^{\prime} B^{\prime} C^{\prime}}=S_{\Delta A B C} \cdot A^{\prime} O=\frac{a^{3} \sqrt{3}}{4}\)
ADMICRO
YOMEDIA
ZUNIA9











