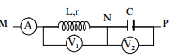
Cho mạch điện RLC có L thay đổi được. Đặt vào hai đầu một điện áp xoay chiều $u={{U}_{0}}\cos \left( 100\pi t+\varphi \right)\text{ }(V).$ Điều chỉnh giá trị của độ tự cảm L ta thấy khi $L={{L}_{1}}=\frac{3}{\pi }\text{ }H$ và $L={{L}_{2}}=\frac{1}{\pi }\text{ H}$ thì dòng điện tức thời i, i tương ứng đều lệch pha một một góc $\frac{\pi }{4}$ so với điện áp hai đầu mạch điện. Tính giá trị của C.

A. $C=\frac{50}{\pi }\text{ }\mu F.$

B. $C=\frac{100}{\pi }\text{ }\mu F$

C. $C=\frac{150}{\pi }\text{ }\mu F$

D. $C=\frac{200}{\pi }\text{ }\mu F$

Sai A là đáp án đúng Xem lời giải

Chính xác Xem lời giải

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

ATNETWORK

Môn: Vật Lý Lớp 12

Chủ đề: Dòng điện xoay chiều

Bài: Mạch R-L-C nối tiếp

Lời giải:

Báo sai

Cảm kháng của cuộn dây ở hai trường hợp: ${{Z}_{L1}}=\omega {{L}_{1}}=300\text{ }\Omega ;\text{ }{{Z}_{L2}}=\omega {{L}_{2}}=100\text{ }\Omega .$

Ta có Z_L1 > Z_L2 và cả hai trường hợp cường độ dòng điện đều lệch pha một một góc $\frac{\pi }{4}$ so với điện áp hai đầu mạch điện => với L₁ mạch có tính cảm kháng (Z_L1 > Z_C), với L₂ mạch có tính dung kháng (Z_L2 < Z_C).

Độ lệch pha giữa u và i khi $L={{L}_{1}}=\frac{3}{\pi }\text{ }H:\tan {{\varphi }_{1}}=\frac{{{Z}_{L1}}-{{Z}_{C}}}{R}=1.$ (1)

Độ lệch pha giữa u và i khi $L={{L}_{2}}=\frac{1}{\pi }\text{ H:}\tan {{\varphi }_{2}}=\frac{{{Z}_{L2}}-{{Z}_{C}}}{R}=-1.$ (2)

Từ (1) và (2) ta có: $\frac{{{Z}_{L1}}-{{Z}_{C}}}{R}=-\frac{{{Z}_{L2}}-{{Z}_{C}}}{R}\Rightarrow {{Z}_{C}}=\frac{{{Z}_{L1}}+{{Z}_{L2}}}{2}=200\text{ }\Omega \text{.}$

Điện dung của tụ điện: $C=\frac{1}{\omega {{Z}_{C}}}=\frac{1}{100\pi .200}=\frac{50}{\pi }{{.10}^{-6}}=\frac{50}{\pi }\text{ }\mu F.$

ADMICRO

YOMEDIA

Câu hỏi liên quan

Một đoạn mạch gồm cuộn dây thuần cảm có độ tự cảm $L=\frac{1}{5\pi }\text{ }H$ mắc nối tiếp với tụ điện có điện dung $C=\frac{{{2.10}^{-4}}}{\pi }\text{ }F.$Dòng điện chạy qua đoạn mạch có biểu thức $i=2\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{3} \right)\text{ }(A).$ Biểu thức điện áp hai đầu đoạn mạch sẽ là
ặt điện áp u = $120\sqrt 2$ cos100πt (V) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm cuộn cảm thuần L mắc nối tiếp với điện trở thuần R, đoạn MB chỉ có tụ điện C. Biết điện áp giữa hai đầu đoạn mạch AM và điện áp giữa hai đầu đoạn mạch MB lệch pha nhau 2π/3. Điện áp hiệu dụng trên AM bằng một nửa trên MB. Điện áp hiệu dụng giữa hai đầu đoạn mạch AM bằng.
Mạch điện như hình vẽ, các vôn kế: V₁ chỉ 75V, V₂ chỉ 125V, $u_{MP}= 100\sqrt 2(cos 100\pi t)V $. Cuộn cảm có điện trở. Cho R_A = 0, $ R_{V1} = R_{V2}=\infty$ Biểu thức điện áp u_MN là:

ZUNIA12

Đặt điện áp $u={{U}_{0}}cos2\pi ft$ (với U₀ không đổi, f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C. Khi $f={{f}_{1}}=25\sqrt{2}\text{ }Hz$ hoặc khi $f={{f}_{2}}=100\text{ }Hz$ thì điện áp hiệu dụng ở hai đầu tụ điện có cùng giá trị U₀. Khi f = f₀ thì điện áp hiệu dụng hai đầu điện trở đạt cực đại. Giá trị của f₀ gần giá trị nào nhất sau đây?
Khi đặt vào hai đầu một cuộn dây có độ tự cảm $\frac{0,4}{\pi }\text{ }H$ một hiệu điện thế một chiều 12 V thì cường độ dòng điện qua cuộn dây là 0,4 A. Sau đó, thay hiệu điện thế này bằng một điện áp xoay chiều có tần số 50 Hz và giá trị hiệu dụng 12 V thì cường độ dòng điện hiệu dụng qua cuộn dây bằng
Đặt một điện thế xoay chiều u = 300cosωt (V) vào hai đầu một đoạn mạch RLC mắc nối tiếp gồm tụ điện có dung kháng Z_C = 200 W, điện trở thuần R = 100 W và cuộn dây thuần cảm có cảm kháng Z_L = 100 W. Cường độ hiệu dụng của dòng điện trong đoạn mạch này bằng
Cho đoạn mạch RLC nối tiếp có ${{U}_{L}}={{U}_{R}}=\frac{{{U}_{C}}}{2}$ thì độ lệch pha giữa điện áp hai đầu đoạn mạch với dòng điện qua mạch là:
Cho đoạn mạch gồm cuộn dây có điện trở thuần R = 100 Ω, hệ số tự cảm $L=\frac{1}{\pi }\text{ }H$ mắc nối tiếp với tụ điện có điện dung $C=\frac{{{10}^{-4}}}{2\pi }\text{ }F.$ Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = 200sin(100πt)V. Biểu thức điện áp tức thời giữa hai đầu cuộn dây là
Đặt hiệu điện thế xoay chiều $u={{U}_{0}}cos(100\pi t+\varphi )\text{ }(V)$ vào hai đầu đoạn mạch nối tiếp theo thứ tự gồm R₁, R₂ và cuộn thuần cảm có độ tự cảm L thay đổi được. Biết ${{\text{R}}_{1}}=2{{\text{R}}_{2}}=200\sqrt{3}\text{ }\Omega .$ Điều chỉnh L cho đến khi hiệu điện thế tức thời giữa hai đầu đoạn mạch chứa R₂ và L lệch pha cực đại so với hiệu điện thế hai đầu đoạn mạch. Giá trị của độ tự cảm lúc đó là?
Một đoạn mạch gồm cuộc dây thuần cảm có độ tự cảm $\text{L}=\frac{\text{1}}{\pi }\text{ H}$ mắc nối tiếp với điện trở thuần R = 100 W. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều $u=100\sqrt{2}\cos \left( 100\pi t \right)\text{ (V)}\text{.}$ Biểu thức cường độ dòng điện trong mạch là
Đặt điện áp $u={{U}_{0}}cos2\pi ft$ ( U₀ không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch có R,L,C nối tiếp. Khi tần số là f₁ thì cảm kháng và dung kháng của đoạn mạch có giá trị lần lượt là 36 W và 144 W. Khi tần số là 120 Hz thì cường độ dòng điện trong đoạn mạch cùng pha với u. Giá trị f₁ là
Đặt điện áp $u={{U}_{0}}cos\omega t$ (với U₀ không đổi, w thay đổi) vào hai đầu đoạn mạch nối tiếp gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C . Khi ω = ω₀ trong mạch có cộng hưởng điện. Tần số góc w₀ là
Cho đoạn mạch gồm điện trở R = 100 Ω, tụ điện $C=\frac{{{10}^{-4}}}{\pi }\text{ }F$ và cuộn cảm $L=\frac{2}{\pi }\text{ }H$ mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều $u=200\cos 100\pi t\text{ }(V).$ Cường độ dòng điện hiệu dụng trong mạch là
Một mạch điện gồm $R=60\text{ }\Omega ,\text{ }L=\frac{0,12}{\pi }\text{ }H,\text{ }C=\frac{1}{200\pi }\text{ }F$ mắc nối tiếp. Cho dòng điện xoay chiều hình sin có tần số f = 50 Hz qua mạch thì tổng trở của đoạn mạch là
Đặt một hiệu điện thế xoay chiều $u={{U}_{0}}\cos \omega t$ vào hai đầu một đoạn mạch điện RLC không phân nhánh. Dòng điện nhanh pha hơn hiệu điện thế ở hai đầu đoạn mạch điện này khi
Trong mạch dao động LC có điện trở thuần bằng không thì:
Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện. Hiệu điện thế hiệu dụng hai đầu đoạn mạch, hai đầu cuộn dây, hai đầu tụ điện đều bằng nhau. Hệ số công suất (cosφ ) của đoạn mạch là:
Phát biểu nào sau đây là không đúng? Trong mạch điện xoay chiều không phân nhánh khi điện dung của tụ điện thay đổi và thoả mãn $\omega =\frac{1}{\sqrt{LC}}$ thì
Đặt điện áp $u={{U}_{0}}cos\left( \omega t-\frac{\pi }{2} \right)(V)$ vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, cường độ dòng điện trong mạch là $i={{I}_{0}}cos\left( \omega t-\frac{2\pi }{3} \right)(A).$ Biết U₀, I₀ và w không đổi. Hệ thức đúng là
Một mạch điện xoay chiều nối tiếp có $R=60\Omega; L= \frac{0,2}{\pi} H; C= \frac{10^{-4}}{\pi} F$ mắc vào mạng điện xoay chiều có chu kì 0,02 s. Tổng trở của đoạn mạch là: