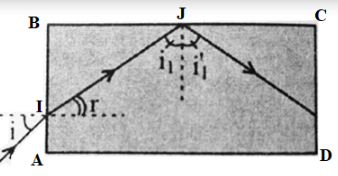
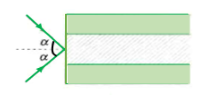
Cho một khối thuỷ tinh hình hộp chữ nhật có tiết diện thẳng ABCD đặt trong không khí. Để mọi tia sáng tới mặt có cạnh AB đều phản xạ toàn phần ở mặt có cạnh BC thì chiết suất n của thuỷ tinh có giá trị nhỏ nhất là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Ta có:\(\left\{ \begin{array}{l} \sin i = n\sin r\\ \sin {i_1} > \sin {i_{gh}} = \frac{1}{n}\\ {i_1} + r = {90^0} \end{array} \right.\)
Do đó:
\(\to \left\{ \begin{array}{l} \sin ({90^0} - r) = \cos r\\ \cos r \ge \frac{1}{n} \end{array} \right. \to \sqrt {1 - {{\sin }^2}r} \ge \frac{1}{n} \to 1 - {\sin ^2}r \ge \frac{1}{{{n^2}}}\)
Mà: \( {\sin ^2}r = \frac{{{{\sin }^2}i}}{{{n^2}}} \to 1 - \frac{{{{\sin }^2}i}}{{{n^2}}} \ge \frac{1}{{{n^2}}} \to {n^2} \ge {\sin ^2}i + 1\)
Mặt khác: \( {\sin ^2}i \ge 1 \to {n^2} \ge 2 \to n \ge \sqrt 2 \)
Câu hỏi liên quan
-
Chọn phương án sai. Chiếu một chùm tia sáng tới mặt phân cách giữa hai môi trường trong suốt. Khi xảy ra hiện tượng phản xạ toàn phần thì:
-
Ánh sáng truyền trong môi truờng có chiết suất n1, tới mặt phân cách với môi trường có chiết suất n2 với góc tới i ≠ 0. Xét các điều kiện sau:
(1) n2 > n1. (2) n2 < n1. (3) sini ≥ n2/n1. (4) sini ≤ n2/n1
Nếu muốn luôn luôn có khúc xạ ánh sáng thì (các) điều kiện là:
-
Ánh sáng truyền từ một môi trường tới môi trường chiết quang kém hơn và góc tới lớn hơn góc giới hạn là điều kiện để có
-
Đổ một chất lỏng mà người ta muốn đo chiết suất vào trong 1 chậu rồi thả nổi trên mặt thoáng 1 đĩa tròn có bán kính 12cm. Tại tâm O của đĩa về phía dưới có một cái kim vuông góc với mặt đĩa, người ta chỉ trông rõ đầu kim khi kim dài hơn 10,6cm. Tính chiết suất của chất lỏng và cho biết chất lỏng đó là chất lỏng gì ?
-
Một sợi quang hình trụ gồm phần lõi có chiết suất n=1,58 và phần vỏ bọc có chiết suất no=1,41. Trong không khí, một tia sáng tới mặt trước của sợi quang tại điểm O (O nằm trên trục của sợi quang) với góc tới α rồi khúc xạ vào phần lõi (như hình bên). Để tia sáng chỉ truyền trong phần lõi thì giá trị lớn nhất của góc α gần nhất với giá trị nào sau đây?
.PNG)
-
Chọn câu trả lời sai. Khi ánh sáng truyền từ môi trường có chiết suất nhỏ sang môi trường có chiết suất lớn thì
-
Sợi quang trong cáp quang ứng dụng hiện tượng
-
Trong sợi quang chiết suất của phần lõi
-
Một khối thủy tinh P có chiết suất (n = 1,5 ). Biết tiết diện thẳng là một tam giác ABC vuông cân tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI. Góc D hợp bởi tia ló và tia tới là:
-
Cho triết suất của nước bằng 1,33, của benzen bằng 1,5, của thuỷ tinh flin là 1,8. Có thể xảy ra hiện tượng phản xạ toàn phần khi chiếu sáng từ môi trường nào sang môi trường nào?
-
Khi tia sáng truyền xiên góc tới mặt phân cách hai môi trường trong suốt khác nhau mà không có tia khúc xạ thì chắc chắn.
-
Lúc trưa nắng, mặt đường nhựa khô ráo, nhưng nhìn từ xa có vẻ như ướt nước. Đó là vì các tia sáng phản xạ
-
Cho chiết suất của nước bằng 4/3, của benzen bằng 1,5; của thủy tinh flin là 1,8. Hiện tượng phản xạ toàn phần không xảy ra khi chiếu ánh sáng từ:
-
Cho ba tia sáng truyền từ không khí đến ba môi trường trong suốt 1, 2, 3 dưới cùng một góc tới i. Biết góc khúc xạ lần lượt là \(r_1, r_2, r_3\) với \(r_1 > r_2 > r_3\). Hiện tượng phản xạ toàn phần không xảy ra khi ánh sáng truyền từ môi trường
-
Một ống dẫn sáng hình trụ với lõi có chiết suất n1 = 1,6 và phần vỏ bọc ngoài có chiết suất \(n_2= \sqrt2\). Chùm tia tới hội tụ tại mặt trước của ống tại điểm I với góc \(2\alpha\). Xác định \(\alpha\) nhỏ nhất để tia sáng trong chùm đều truyền được trong ống.
-
Chiếu một chùm tia sáng tới mặt phân cách giữa hai môi trường trong suốt. Khi xảy ra hiện tượng phản xạ toàn phần thì
-
Một miếng gỗ mỏng hình tròn, bán kính 4cm. Tại tâm O của miếng gỗ có cắm thẳng góc một cái đinh OA. Thả miếng gỗ nổi trong một chậu nước có chiết suất n = 4/3. Đỉnh OA ở trong nước. Mắt đặt trong không khí, chiều dài lớn nhất của đỉnh OA để mắt không thấy đầu A của đinh xấp xỉ là
-
Một sợi quang hình trụ gồm phần lõi có chiết suất n = 1,51 và phần vỏ bọc có chiết suất no = 1,41. Trong không khí, một tia sáng tới mặt trước của sợi quang tại điểm O (O nằm trên trục của sợi quang) với góc tới α rồi khúc xạ vào phần lõi (như hình bên). Để tia sáng chỉ truyền trong phần lõi thì giá trị lớn nhất của góc α gần nhất với giá trị nào sau đây?
-
Một đĩa tròn mỏng bằng gỗ, bán kính R = 5cm nổi trên mặt nước. Ở tâm đĩa có gắn một cây kim, thẳng đứng, chìm trong nước có chiết suất n = 4/3. Dù đặt mắt ở đâu cũng không thấy cây kim. Chiều dài tối đa của cây kim là:
-
Một khối thủy tinh P có chiết suất n đặt trong không khí. Tiết diện thẳng là một tam giác cân ABC vuông tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI thì tia sáng đi là là mặt AC. Xác định chiết suất n của khối chất P
