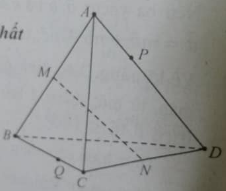
Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD . Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{M N}=k(\overrightarrow{A C}+\overrightarrow{B D})\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\overrightarrow{M N}=\frac{1}{2}(\overrightarrow{M C}+\overrightarrow{M D}) \text { (quy tắc trung điểm) }=\frac{1}{2}(\overrightarrow{M A}+\overrightarrow{A C}+\overrightarrow{M B}+\overrightarrow{B D})\)
Mà \(\overrightarrow{M A}+\overrightarrow{M B}=\overrightarrow{0} \text { (vì } M \text { là trung điểm } A B) \Rightarrow \overrightarrow{M N}=\frac{1}{2}(\overrightarrow{A C}+\overrightarrow{B D})\)
Câu hỏi liên quan
-
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;2;−1); B(2;−1;3), C(−4;7;5). Tọa độ chân đường phân giác trong góc B của tam giác ABC là:
-
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Vecto \(\overrightarrow {B'C} \) bằng:
-
Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Đặt \(\vec{x}=\overrightarrow{A B} ; \vec{y}=\overrightarrow{A C} ; \vec{z}=\overrightarrow{A D}\) . Khẳng định nào sau đây đúng
-
Trong không gian cho điểm O và bốn điểm A , B , C , D không thẳng hàng. Điều kiện cần và đủ để A , B , C , D tạo thành hình bình hành là
-
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA'} \; = \;\vec a,\;\overrightarrow {AB} \; = \;\vec b,\;\overrightarrow {AC} \; = \;\vec c\)
Vecto \(\overrightarrow {AG} \) bằng:
-
Cho tứ diện ABCD . Gọi P, Q là trung điểm của AB và CD . Chọn khẳng định đúng
-
Cho ba vectơ\(\vec{a}, \vec{b}, \vec{c}\) không đồng phẳng. Trong các khẳng định sau, khẳng định nào sai?
-
Cho tứ diện ABCD . Đặt \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A C}=\vec{b}, \overrightarrow{A D}=\vec{c}\),gọi M là trung điểm của BC. Trong các khẳng định sau, khẳng định nào đúng?
-
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;4;2), B(−1;2;4). Tìm tọa độ điểm M thuộc trục Oz sao cho :MA2+MB2 = 32.
-
Cho tứ diện ABCD có AB = AC = AD; góc BAC = góc BAD = 60oBAD = 60o. Hãy chứng mình AB ⊥ CD.
Một bạn chứng mình qua các bước sau:
Bước 1. \(\overrightarrow {CD} \; = \;\overrightarrow {AC} \; - \;\overrightarrow {AD} \)
Bước 2. \(\overrightarrow {AB} .\overrightarrow {CD} \; = \;\overrightarrow {AB} .\left( {\overrightarrow {AC} \; - \;\overrightarrow {AD} } \right)\)
Bước 3. \(\overrightarrow {AB} .\overrightarrow {AC} \; - \;\overrightarrow {AB} .\overrightarrow {AD} \; = \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} \;} \right|.\cos {60^o}\; - \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} } \right|.\cos {60^o}\; = \;0\)
Bước 4. Suy ra AB ⊥ CD
Theo em. Lời giải trên sai từ:
-
Cho ba vectơ \(\vec{a}, \vec{b}, \vec{c}\) không đồng phẳng. Xét các vectơ \(\vec{x}=2 \vec{a}+\vec{b} ; \vec{y}=\vec{a}-\vec{b}-\vec{c} ; \vec{z}=-3 \vec{b}-2 \vec{c}\).Chọn khẳng định đúng?
-
Cho tứ diện ABCD . Đặt \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A C}=\vec{b}, \overrightarrow{A D}=\vec{c}\) gọi G là trọng tâm của tam giác BCD . Trong các đẳng thức sau, đẳng thức nào đúng?
-
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt \(\vec{x}=\overrightarrow{A B} ; \vec{y}=\overrightarrow{A C} ; \vec{z}=\overrightarrow{A D}\) . Khẳng
định nào sau đây đúng? -
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60o. Gọi M và N là trung điểm của AB và CD
Kết luận nào sau đây sai?
-
Cho hai điểm phân biệt A, B và một điểm O bất kỳ không thuộc đường thẳng AB . Mệnh đề nào sau đây là đúng?
-
Trong không gian với hệ tọa độ Oxyz, các điểm A(1;2;3),B(3;3;4),C(−1;1;2) sẽ:
-
Trong không gian với hệ tọa độ Oxyz , để hai vecto \(\overrightarrow a = (m;2;3);\overrightarrow b = (1;n;2)\) cùng phương thì (2m + 3n ) bằng.
-
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60o. Gọi M và N là trung điểm của AB và CD
Góc giữa \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) bằng:
-
Cho hình lăng trụ tam giác\(A B C A^{\prime} B^{\prime} C^{\prime}.\). Đặt \(\overrightarrow{A A^{\prime}}=\vec{a}, \overrightarrow{A B}=\vec{b}, \overrightarrow{A C}=\vec{c}, \overrightarrow{B C}=\vec{d}.\) Trong các biểu
thức véctơ sau đây, biểu thức nào đúng -
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt \(\overrightarrow{S A}=\vec{a} ; \overrightarrow{S B}=\vec{b} ; \overrightarrow{S C}=\vec{c},\overrightarrow{S D}=\vec{d}\). Khẳng định nào sau đây đúng?
