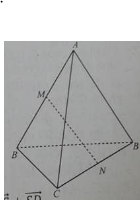
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Đặt \(\overrightarrow{S A}=\vec{a}, \overrightarrow{S B}=\vec{b}, \overrightarrow{S C}=\vec{c}, \overrightarrow{S D}=\vec{d}\). Khẳng định nào sau đây đúng.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi O là tâm của hình bình hành ABCD. Ta có:
\(\left\{\begin{array}{l} \vec{a}+\vec{c}=\overrightarrow{S A}+\overrightarrow{S C}=2 \overrightarrow{S O} \\ \vec{b}+\vec{d}=\overrightarrow{S B}+\overrightarrow{S D}=2 \overrightarrow{S O} \end{array}=>\vec{a}+\vec{c}=\vec{d}+\vec{b}\right.\)
Câu hỏi liên quan
-
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;4;2), B(−1;2;4). Tìm tọa độ điểm M thuộc trục Oz sao cho :MA2+MB2 = 32.
-
Cho hình hộp \(A B C D \cdot A_{1} B_{1} C_{1} D_{1}\) . Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{A B}+\overrightarrow{B_{1} C_{1}}+\overrightarrow {D D_{1}}=k \overrightarrow {A C_{1}}\)
-
Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{M N}=k(\overrightarrow{A D}+\overrightarrow{B C})\)
-
Cho ba vecto \(\vec a,\;\vec b,\;\vec c\). Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
-
Cho hình lăng trụ tam giác \(A B C \cdot A_{1} B_{1} C\). Đặt \(\overrightarrow{A A_{1}}=\vec{a}, \overrightarrow{A B}=\vec{b}, \overrightarrow{A C}=\vec{c}, \overrightarrow{B C}=\vec{d}\). Trong các đẳng
thức sau, đẳng thức nào đúng? -
Cho tứ diện ABCD có AB = AC = AD; góc BAC = góc BAD = 60oBAD = 60o. Hãy chứng mình AB ⊥ CD.
Một bạn chứng mình qua các bước sau:
Bước 1. \(\overrightarrow {CD} \; = \;\overrightarrow {AC} \; - \;\overrightarrow {AD} \)
Bước 2. \(\overrightarrow {AB} .\overrightarrow {CD} \; = \;\overrightarrow {AB} .\left( {\overrightarrow {AC} \; - \;\overrightarrow {AD} } \right)\)
Bước 3. \(\overrightarrow {AB} .\overrightarrow {AC} \; - \;\overrightarrow {AB} .\overrightarrow {AD} \; = \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} \;} \right|.\cos {60^o}\; - \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} } \right|.\cos {60^o}\; = \;0\)
Bước 4. Suy ra AB ⊥ CD
Theo em. Lời giải trên sai từ:
-
Trong không gian với hệ tọa độ Oxyz , để hai vecto \(\overrightarrow a = (m;2;3);\overrightarrow b = (1;n;2)\) cùng phương thì (2m + 3n ) bằng.
-
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho \(\overrightarrow {PA} \; = \;m\overrightarrow {PD} \) và \(\overrightarrow {QB} \; = \;m\overrightarrow {QC} \), với m khác 1. Vecto \(\overrightarrow {MP}\) bằng:
-
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tâm O . Gọi I là tâm hình bình hành ABCD . Đặt \(\overrightarrow {A C^{\prime}}=\vec{u},\overrightarrow{C A^{\prime}}=\vec{v}, \overrightarrow{B D^{\prime}}=\vec{x}, \overline{D B^{\prime}}=\bar{y}\) . Trong các đẳng thức sau, đẳng thức nào đúng?
-
Ba vecto \(\vec a,\;\vec b,\;\vec c\) không đồng phẳng nếu?
-
Cho ba vecto \(\vec n,\;\vec a,\;\vec b\) bất kì đều khác với vecto \(\vec 0\). Nếu vecto \(\vec n\) vuông góc với cả hai vecto \(\vec a\) và \(\vec b\) thì \(\vec n\), \(\vec a\) và \(\vec b\):
-
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A′B′C′D′ biết A(1;0;1), B(2;1;2), D(1;−1;1) và C′(4;5;−5). Khi đó, thể tích của hình hộp đó là:
-
Cho A(1;2;5),B(1;0;2),C(4;7;−1),D(4;1;a). Để 4 điểm A,B,C,D đồng phẳng thì a bằng:
-
Cho ΔABC có A(0;−2), B(4;0),C(1;1) và G là trọng tâm. Điểm M thuộc đường thẳng y = 2 sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất, khi đó tọa độ \(\overrightarrow {MG} \) là
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Từ A hạ AH ⊥ SM. Khi đó góc giữa hai vecto \(\overrightarrow {SA} \) và \(\overrightarrow {AH} \) bằng:
.png)
-
Cho lăng trụ tam giác \(A B C \cdot A^{\prime} B^{\prime} C^{\prime} \text { có } \overrightarrow{A A^{\prime}}=\vec{a}, \overrightarrow{A B}=\vec{b}, \overrightarrow{A C}=\vec{c}\). Hãy phân tích (biểu thị) vectơ \(\overrightarrow{B C^{\prime}}\) qua các vectơ \(\vec{a}, \vec{b}, \vec{c}\)
-
Cho hai điểm phân biệt A, B và một điểm O bất kỳ không thuộc đường thẳng AB . Mệnh đề nào sau đây là đúng?
-
Cho hình lập phương ABCD.EFGH có cạnh bằng a . Ta có \( \overrightarrow{A B} \cdot \overrightarrow{E G}\) bằng?
-
Hãy chọn mệnh đề đúng trong các mệnh đề sau đây:
-
Trong không gian cho điểm O và bốn điểm A , B , C , D không thẳng hàng. Điều kiện cần và đủ để A , B , C , D tạo thành hình bình hành là
